Last updated: 2022-04-20

Checks: 7 0

Knit directory: veg_alcontar/

This reproducible R Markdown analysis was created with workflowr (version 1.7.0). The Checks tab describes the reproducibility checks that were applied when the results were created. The Past versions tab lists the development history.

R Markdown file: up-to-date

Great! Since the R Markdown file has been committed to the Git repository, you know the exact version of the code that produced these results.

Environment: empty

Great job! The global environment was empty. Objects defined in the global environment can affect the analysis in your R Markdown file in unknown ways. For reproduciblity it’s best to always run the code in an empty environment.

Seed: set.seed(20211007)

The command set.seed(20211007) was run prior to running the code in the R Markdown file. Setting a seed ensures that any results that rely on randomness, e.g. subsampling or permutations, are reproducible.

Session information: recorded

Great job! Recording the operating system, R version, and package versions is critical for reproducibility.

Cache: none

Nice! There were no cached chunks for this analysis, so you can be confident that you successfully produced the results during this run.

File paths: relative

Great job! Using relative paths to the files within your workflowr project makes it easier to run your code on other machines.

Repository version: 95151d5

Great! You are using Git for version control. Tracking code development and connecting the code version to the results is critical for reproducibility.

The results in this page were generated with repository version 95151d5. See the Past versions tab to see a history of the changes made to the R Markdown and HTML files.

Note that you need to be careful to ensure that all relevant files for the analysis have been committed to Git prior to generating the results (you can use wflow_publish or wflow_git_commit). workflowr only checks the R Markdown file, but you know if there are other scripts or data files that it depends on. Below is the status of the Git repository when the results were generated:


Ignored files:
    Ignored:    .Rhistory
    Ignored:    .Rproj.user/
    Ignored:    analysis/.DS_Store

Untracked files:
    Untracked:  analysis/compara_methods_SUDOE_files/

Note that any generated files, e.g. HTML, png, CSS, etc., are not included in this status report because it is ok for generated content to have uncommitted changes.

These are the previous versions of the repository in which changes were made to the R Markdown (analysis/compara_methods_SUDOE.Rmd) and HTML (docs/compara_methods_SUDOE.html) files. If you’ve configured a remote Git repository (see ?wflow_git_remote), click on the hyperlinks in the table below to view the files as they were in that past version.

File	Version	Author	Date	Message
Rmd	95151d5	ajpelu	2022-04-20	include new analysis
html	968eb41	ajpelu	2022-04-19	Build site.
Rmd	4104f26	ajpelu	2022-04-19	add new correlations
html	8f01211	ajpelu	2022-04-19	Build site.
Rmd	1b5a50d	ajpelu	2022-04-19	add analysis diversidad
html	3648c33	ajpelu	2022-04-19	Build site.
Rmd	a5285f3	ajpelu	2022-04-19	add analysis diversidad
html	bf70f7c	ajpelu	2022-04-19	Build site.
Rmd	586d4b9	ajpelu	2022-04-19	add new analysis organized

1 Objetivo 1. Carga de combustible: cobertura y fitovolumen

1.1 Cobetura

Vamos a realizar la comparación seleccionando para cada parcela (n=12) un valor de cobertura de quadrats (quadrats medio).

1.1.1 Summary values

Table 1.1: Cobertura || Summary
metodo	mean	sd	se	cv	median	min	max	n
line_intercept	27.19	6.49	1.87	23.86	29.67	11.95	34.0	12
point_quadrat	55.50	7.62	2.20	13.73	56.00	41.00	64.0	12
quadrat medio	29.92	5.35	1.54	17.88	30.81	21.25	37.5	12

1.1.2 Comparación de métodos

ANOVA Kruskal Wallis

Table 1.2: Cobertura || Non-parametric Kruskal-Wallis ANOVA
statistic	p.value	parameter	method	mi_variable
23.84398	6.6e-06	2	Kruskal-Wallis rank sum test	cobertura

Los resultados de la ANOVA no paramétrica (Kruskal-Wallis) indican que existen diferencias significativas para la cobertura (%) entre los diferentes métodos de campo empleados (\(\chi^2\) = 23.84; p<0.0001) (Tabla 1.2).

Posteriormente, evaluamos si existen diferencias entre cada uno de los métodos (post hoc) y observamos que existen diferencias significativas entre el point quadrat y los otros métodos (line intercept y quadrat medio) (Tabla 1.3, Figura 1.1). Asimismo, no observamos diferencias entre la cobertura estimada según el line intercept y el quadrat medio.

Table 1.3: Cobertura || Non-parametric Kruskal-Wallis ANOVA - Post-hoc Dunn’s-test with Bonferroni adjustment
H0	statistic	p.value
line_intercept = point_quadrat	4.53	<0.001
line_intercept = quadrat medio	0.70	>0.999
point_quadrat = quadrat medio	3.84	<0.001

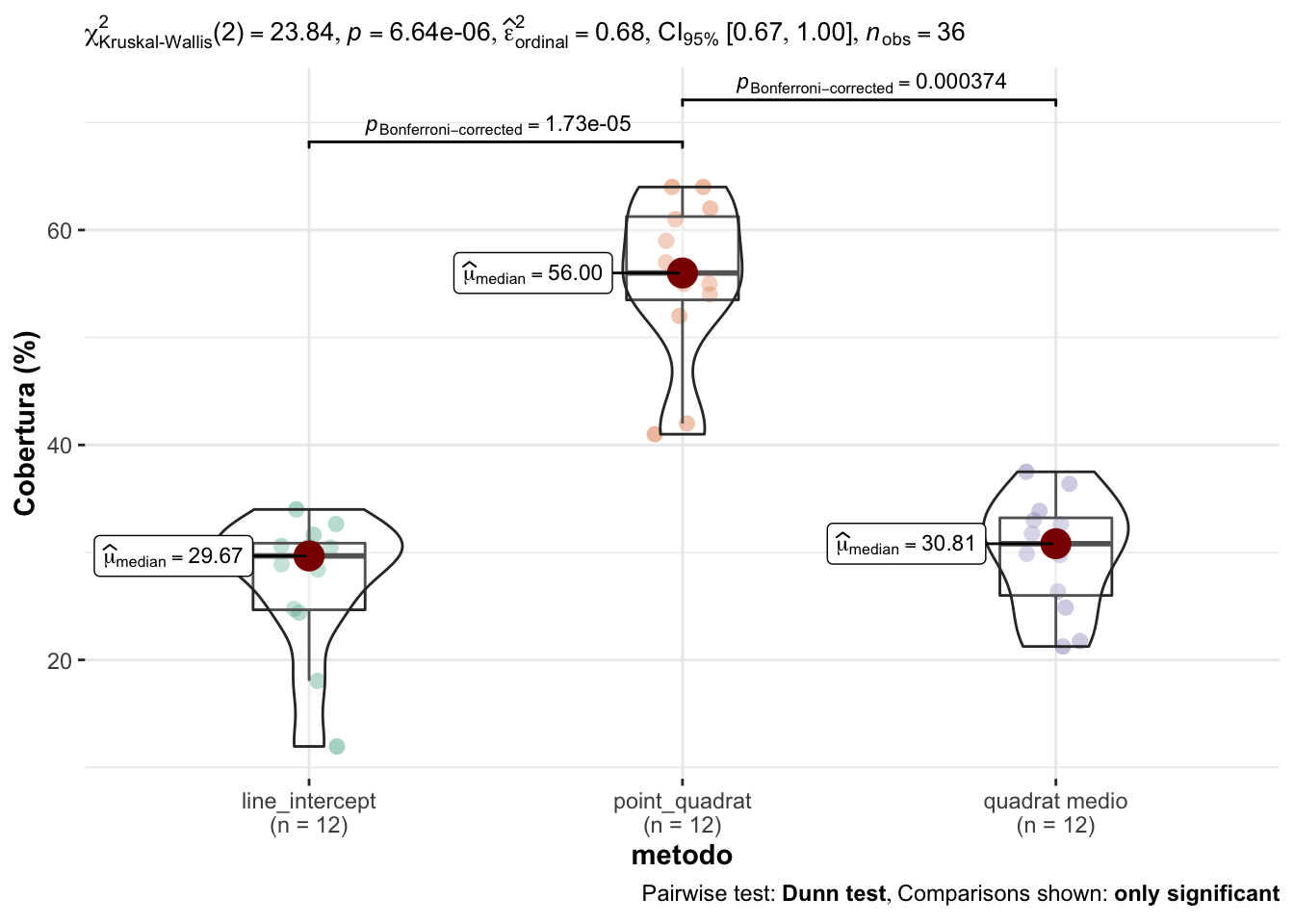
Figure 1.1: Comparación de los valores de cobertura entre los diferentes métodos de campo.

Version	Author	Date
bf70f7c	ajpelu	2022-04-19

1.1.3 Correlación

El siguiente paso es evaluar la correlación que existe entre los métodos de campo para la cobertura.

Tal y como observamos en la Figura 1.2, existe una correlación significativa del line intercept con el point quadrat (\(R^2=\) 0.63), aunque lejos del ajuste perfecto (línea negra en Figura 1.2). El método point quadrat sobreestima los valores de cobertura con respecto al método de line intercept. Así, el rango de cobertura estimado por el LI varía entre 11.95-34 %, mientras que la estimación por PQ varía entre 41-64% (Tabla 1.1). La correlación entre quadrat medio y point quadrat es muy baja (Figura 1.3).

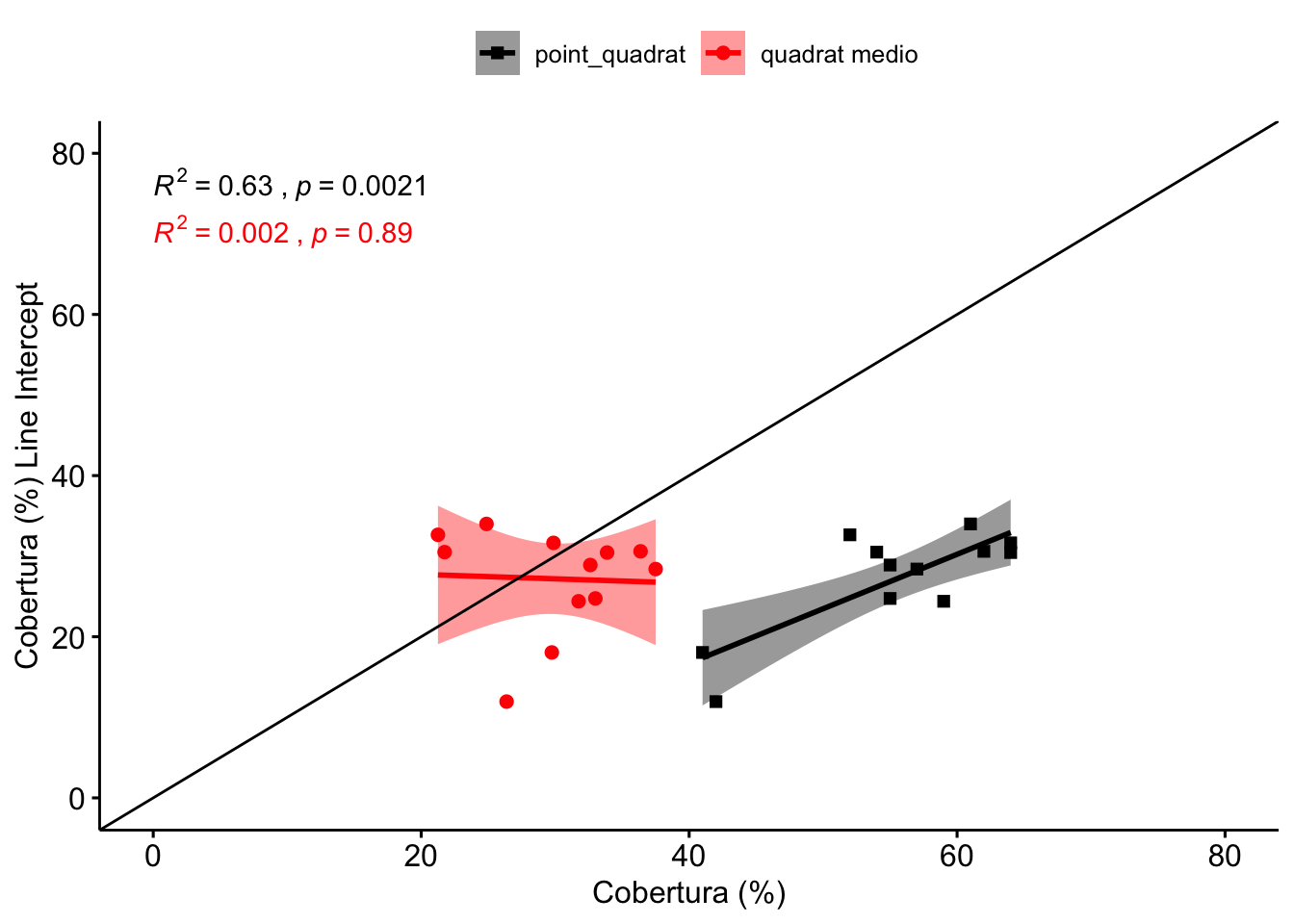
Figure 1.2: Correlación entre los valores de cobertura estimados por Line Intercept y los otros métodos de campo: Point Quadrat y Quadrat medio.

Version	Author	Date
bf70f7c	ajpelu	2022-04-19

1.1.3.1 Correlación Quadrat medio - Point Quadrat

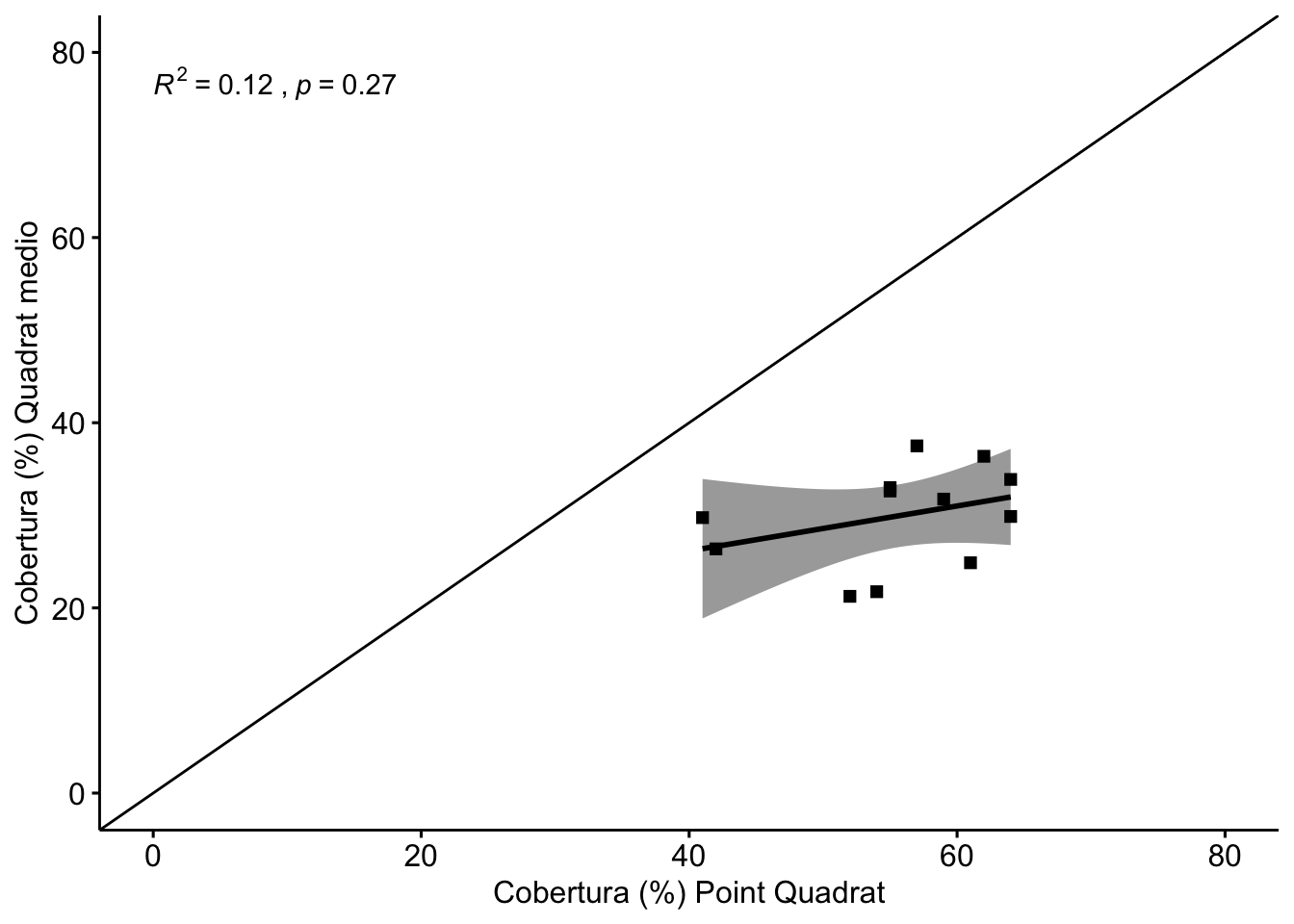
Figure 1.3: Correlación entre los valores de cobertura estimados por Quadrat medio y Point Quadrat.

1.2 Fitovolumen

En este caso solo compararemos los métodos de Line Intercept y Quadrat medio

1.2.1 Summary values

Table 1.4: Fitovolumen || Summary
metodo	mean	sd	se	cv	median	min	max	n
line_intercept	531.04	274.90	79.36	51.77	543.13	84.27	1016.86	12
quadrat medio	778.57	275.23	79.45	35.35	699.70	324.04	1296.47	12

1.2.2 Comparación de métodos

Hemos comprobado Normalidad (W = 0.97; p=0.6350); y homocedasticidad (Bartlett’s K-squared = 0; p=0.9969) y se puede aplicar un método paramétrico, en este caso, la t-student de comparación de medias. Observamos que existen diferencias (Figura 1.4):



The Welch Two Sample t-test testing the difference of value by metodo (mean in group line_intercept = 531.04, mean in group quadrat medio = 778.57) suggests that the effect is negative, statistically significant, and large (difference = -247.53, 95% CI [-480.42, -14.64], t(22.00) = -2.20, p = 0.038; Cohen's d = -0.94, 95% CI [-1.81, -0.05])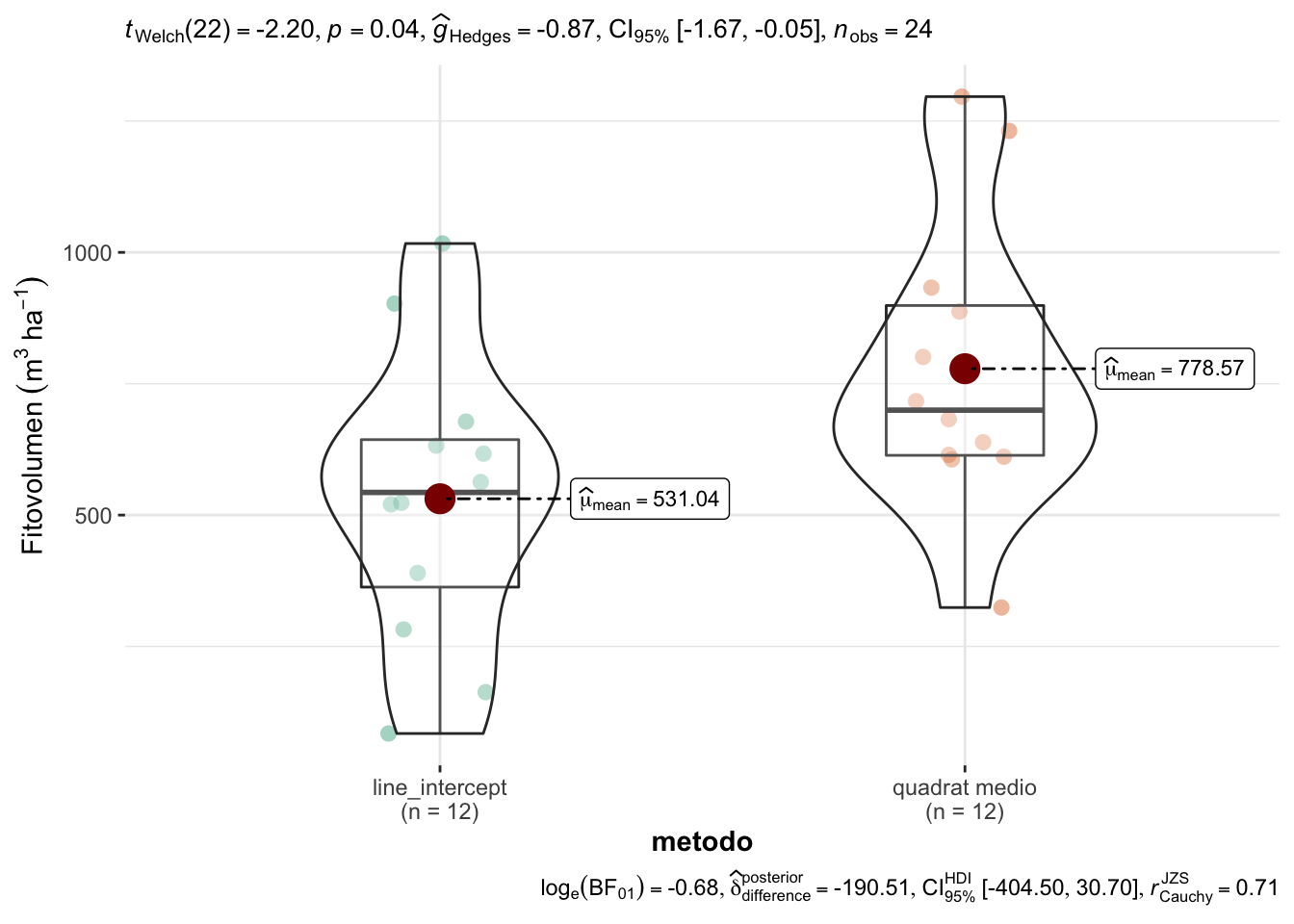

Figure 1.4: Comparación de los valores de fitovolumen entre Line Intercept y Quadrat medio.

Version	Author	Date
bf70f7c	ajpelu	2022-04-19

1.2.3 Correlación

No existe una buena correlación entre los valores de fitovolumen estimados con line intercept y los estimados con quadrat medio (Figura 1.5). Este último método sobreestima el fitovolumen registrado por el LI (ver Tabla 1.4).

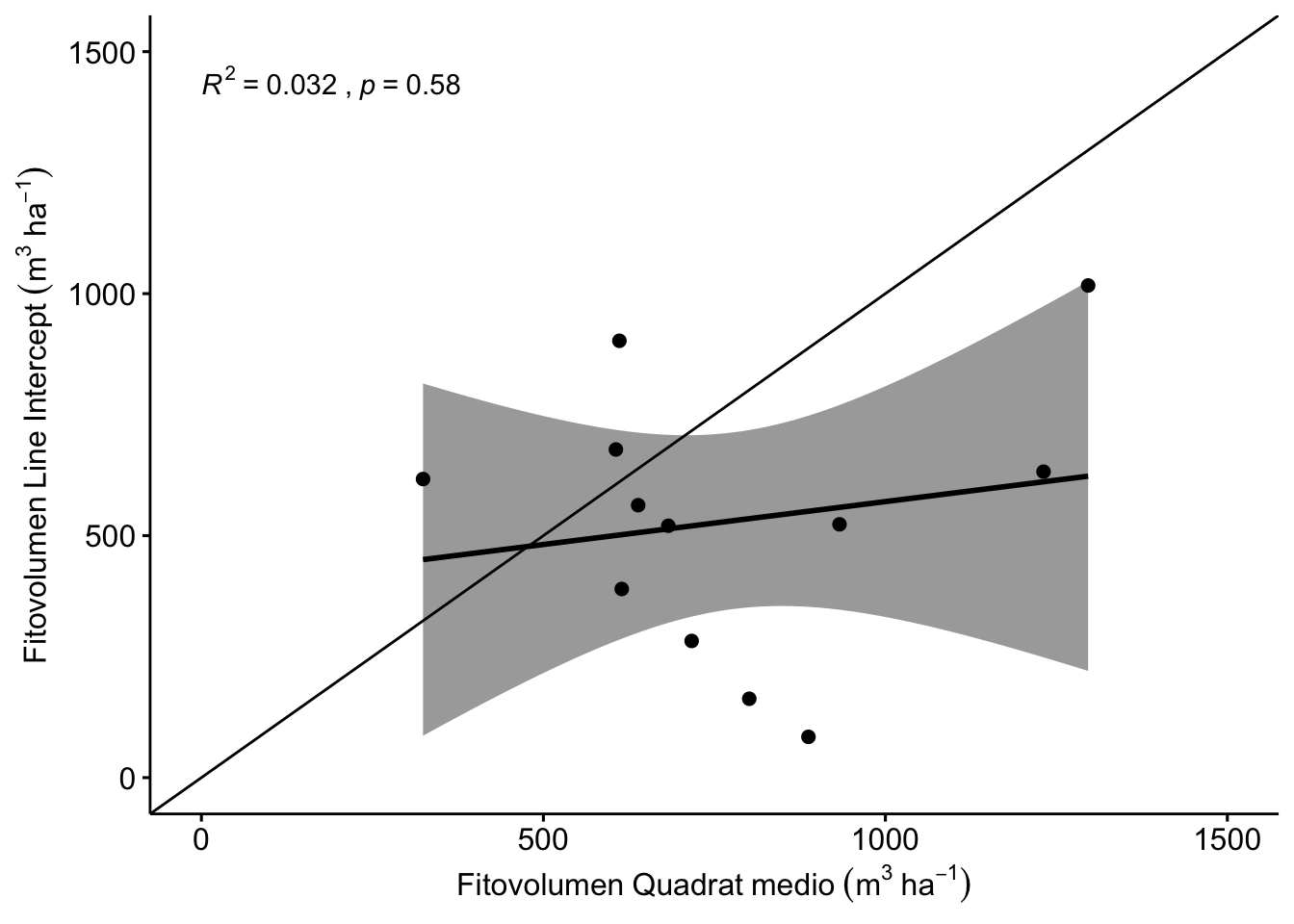
Figure 1.5: Correlación entre los valores de fitovolumen estimados por Line Intercept y Quadrat medio.

Version	Author	Date
bf70f7c	ajpelu	2022-04-19

2 Objetivo 2. Diversidad y Riqueza

2.1 Riqueza

Comparamos entre line intercept, quadrat parcela y point quadrat.

2.1.1 Summary values

Table 2.1: Riqueza || Summary
metodo	mean	sd	se	cv	median	min	max	n
line_intercept	13.00	3.10	0.90	23.88	13.0	8	18	12
point_quadrat	13.17	4.24	1.22	32.20	14.0	7	20	12
quadrat_parcela	34.08	10.39	3.00	30.48	34.5	19	52	12

2.1.2 Comparación de métodos

ANOVA Kruskal Wallis

Table 2.2: Riqueza || Non-parametric Kruskal-Wallis ANOVA
statistic	p.value	parameter	method	mi_variable
22.86057	1.09e-05	2	Kruskal-Wallis rank sum test	riqueza

Los resultados de la ANOVA no paramétrica (Kruskal-Wallis) indican que existen diferencias significativas para la riqueza de especies vegetales entre los diferentes métodos de campo empleados (\(\chi^2\) = 22.86; p<0.0001) (Tabla 2.2).

Posteriormente, evaluamos si existen diferencias entre cada uno de los métodos (post hoc) y observamos que existen diferencias significativas entre el quadrat parcela y los otros métodos (line intercept y point quadrat) (Tabla 2.3, Figura 2.1). Asimismo, no observamos diferencias entre la riqueza estimada según el line intercept y el point quadrat.

Table 2.3: Riqueza || Non-parametric Kruskal-Wallis ANOVA - Post-hoc Dunn’s-test with Bonferroni adjustment
H0	statistic	p.value
line_intercept = point_quadrat	0.02	>0.999
line_intercept = quadrat_parcela	4.15	<0.001
point_quadrat = quadrat_parcela	4.13	<0.001

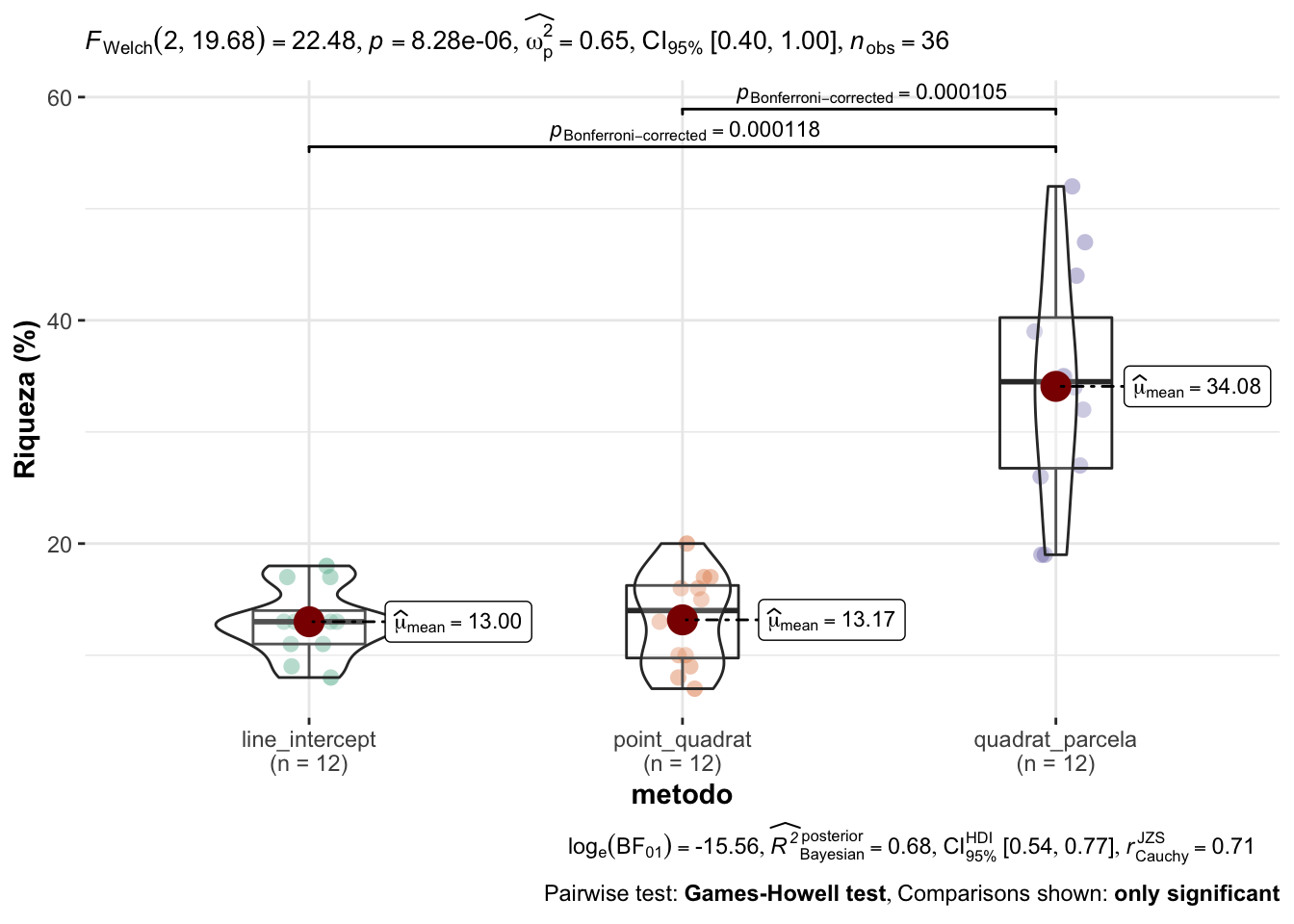
Figure 2.1: Comparación de los valores de riqueza entre los diferentes métodos de campo.

Version	Author	Date
3648c33	ajpelu	2022-04-19

2.1.3 Correlación

Tal y como observamos en la Figura 2.2, los métodos de line intercept y point quadrat, subestiman la riqueza estimada por el método quadrat parcela. Asimismo observamos una buena correlación entre la riqueza estimada por line intercept y point quadrat (Figura 2.3) (\(R^2=\) 0.66).

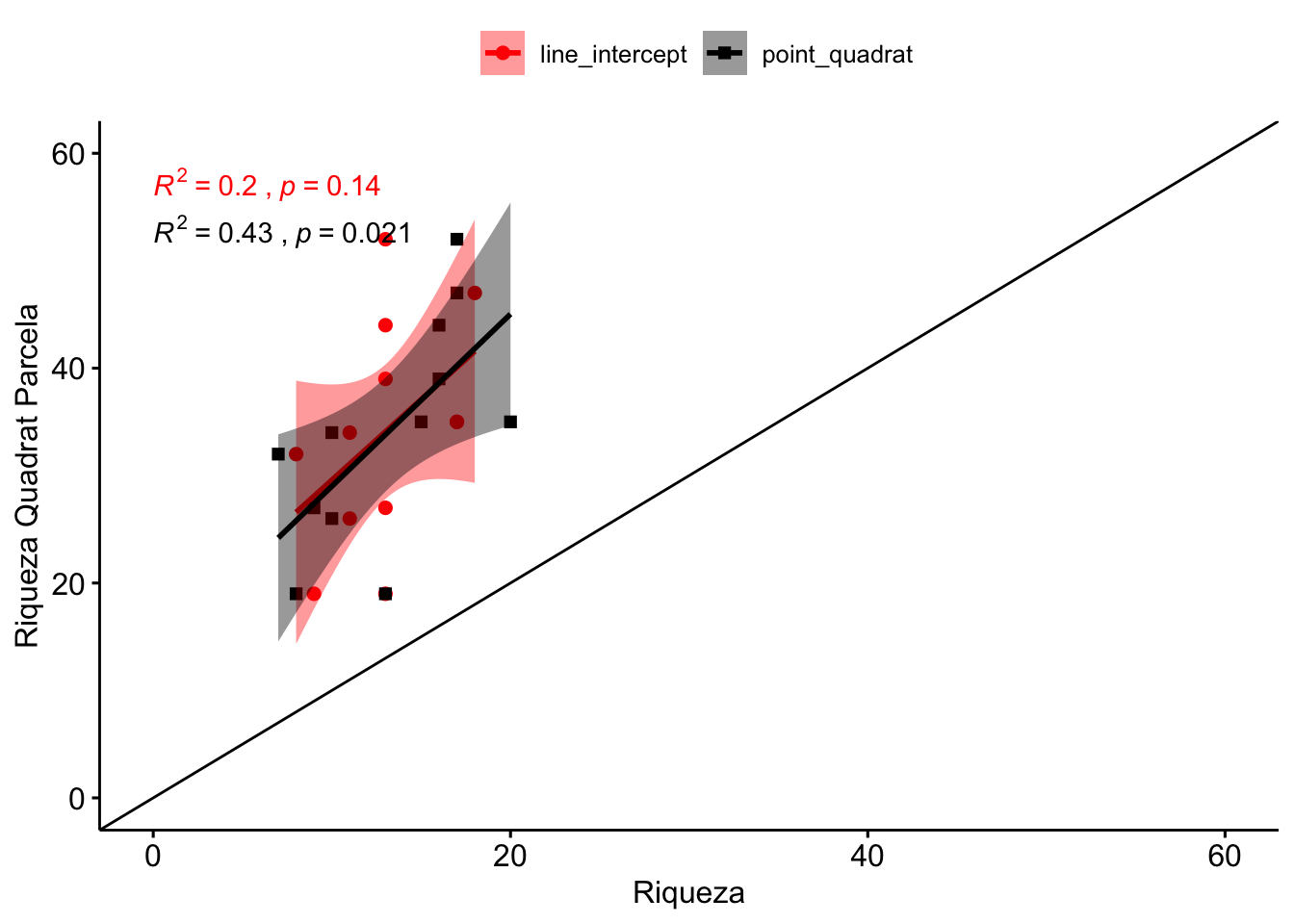
Figure 2.2: Correlación entre los valores de riqueza estimados por Quadrat Parcela y los otros métodos de campo: Line Intercept y Point Quadrat

Version	Author	Date
8f01211	ajpelu	2022-04-19
3648c33	ajpelu	2022-04-19

2.1.3.1 Correlación Line Intercept - Point Quadrat

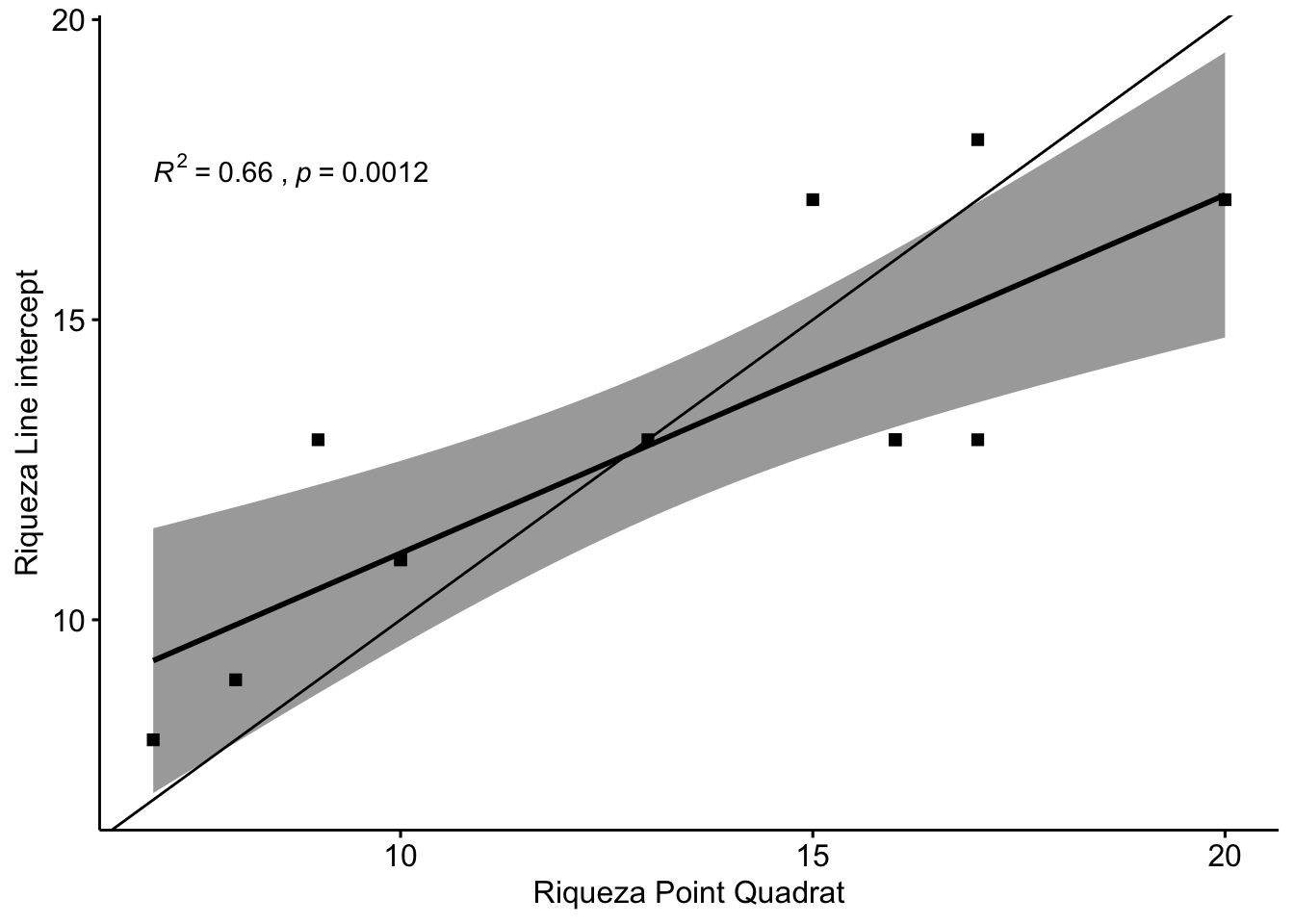
Figure 2.3: Correlación entre los valores de riqueza estimados por Line Intercept y Point Quadrat

2.2 Diversidad

Comparamos entre line intercept, quadrat medio y point quadrat.

2.2.1 Summary values

Table 2.4: Diversidad (Shannon Index) || Summary
metodo	mean	sd	se	cv	median	min	max	n
line_intercept	1.72	0.49	0.14	28.71	1.63	1.10	2.80	12
point_quadrat	1.99	0.45	0.13	22.82	1.95	1.31	2.68	12
quadrat medio	1.34	0.20	0.06	14.78	1.38	0.97	1.58	12

2.2.2 Comparación de métodos

ANOVA Kruskal Wallis

Table 2.5: Diversidad || Non-parametric Kruskal-Wallis ANOVA
statistic	p.value	parameter	method	mi_variable
11.47748	0.0032188	2	Kruskal-Wallis rank sum test	diversidad

Posteriormente, evaluamos si existen diferencias entre cada uno de los métodos (post hoc) y observamos que solamente existen diferencias significativas entre el point quadrat y el quadrat medio (Tabla 2.6, Figura 2.4).

Table 2.6: Diversidad || Non-parametric Kruskal-Wallis ANOVA - Post-hoc Dunn’s-test with Bonferroni adjustment
H0	statistic	p.value
line_intercept = point_quadrat	1.39	0.489
line_intercept = quadrat medio	1.98	0.144
point_quadrat = quadrat medio	3.37	0.002

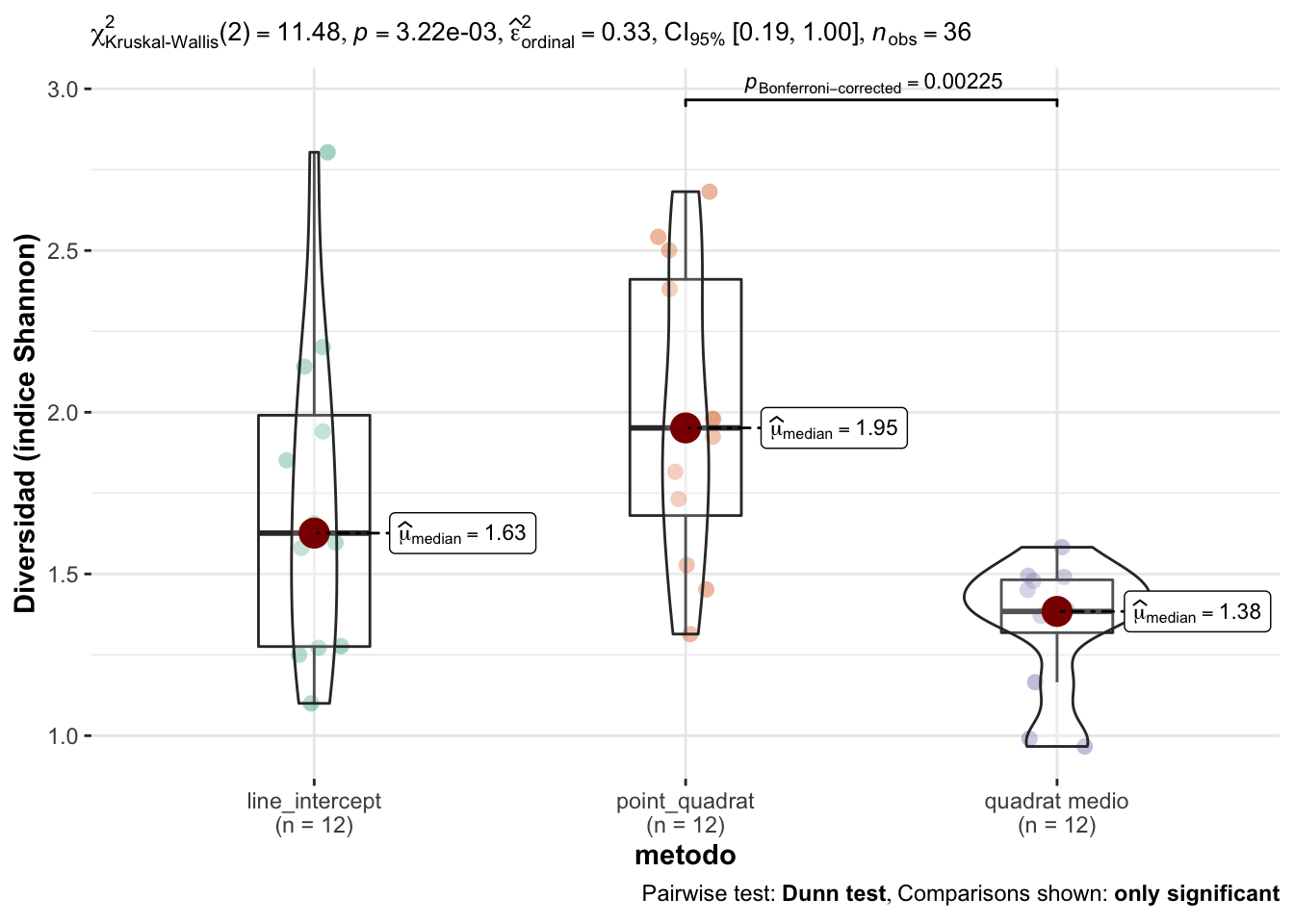
Figure 2.4: Comparación de los valores de diversidad (Shannon) entre los diferentes métodos de campo.

Version	Author	Date
3648c33	ajpelu	2022-04-19

2.2.3 Correlación

El método line intercept subestima la diversidad en comparación con el método point quadrat (Figura 2.5), aunque presentan una significativa y alta correlación (\(R^2=\) 0.82); mientras que el LI sobreestima la diversidad en comparación con el método quadrat medio. La correlación entre point quadrat y quadrat medio es baja (Figura 2.6).

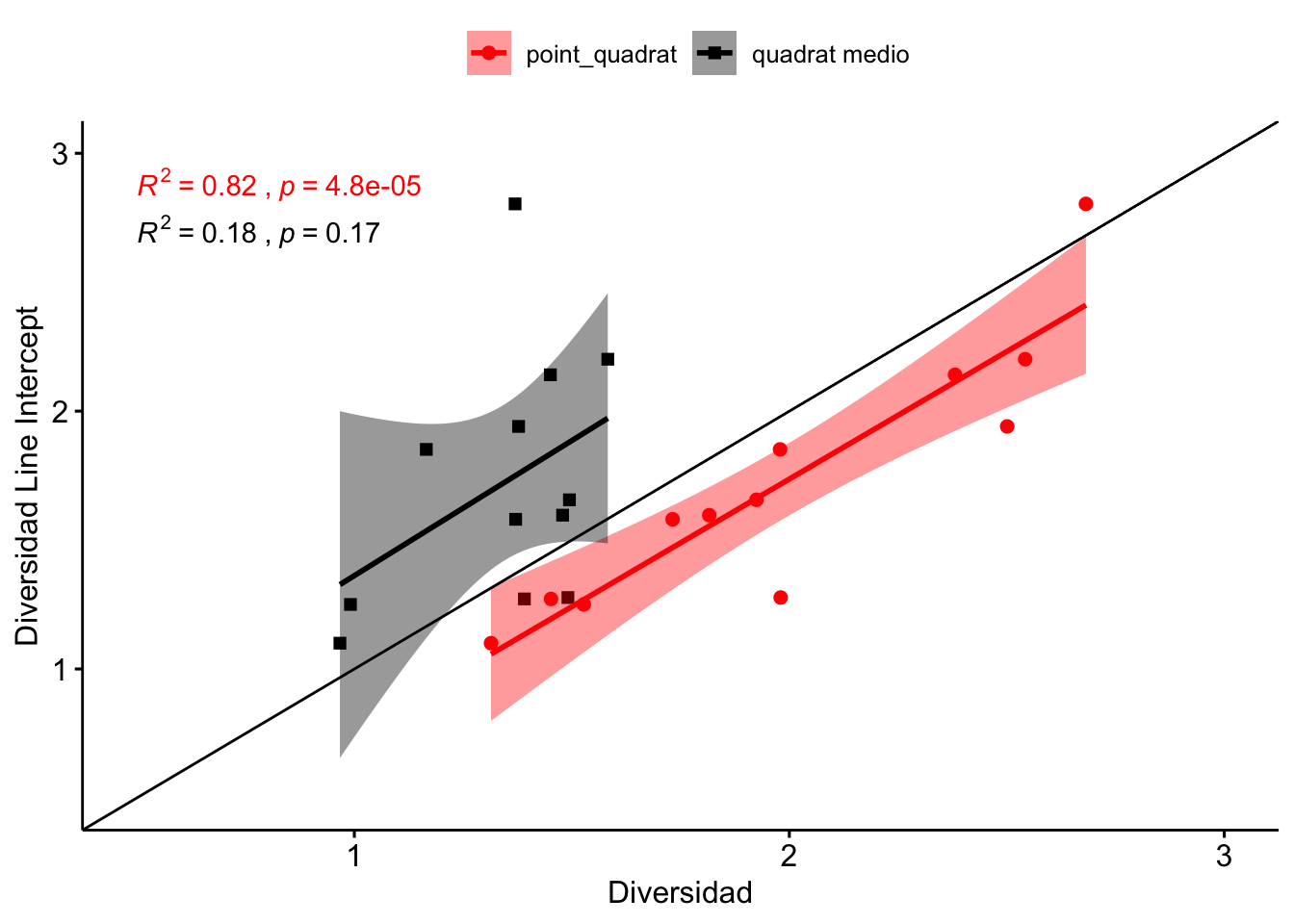
Figure 2.5: Correlación entre los valores de diversidad estimados por Line Intercept y los otros métodos de campo: Point Quadrat y Quadrat Medio

Version	Author	Date
8f01211	ajpelu	2022-04-19
3648c33	ajpelu	2022-04-19

2.2.3.1 Correlación Quadrat Medio - Point Quadrat

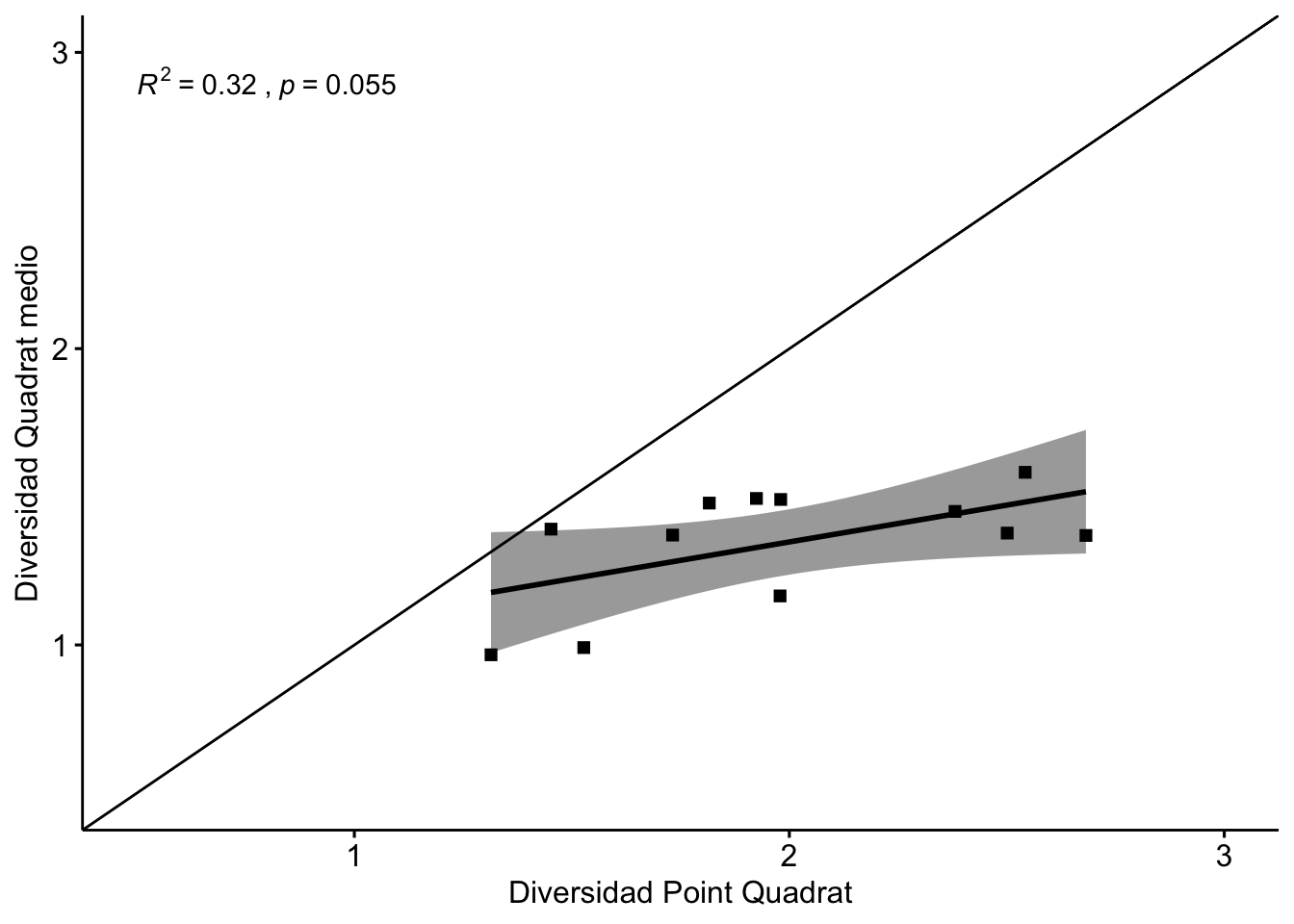
Figure 2.6: Correlación entre los valores de diversidad estimados por Quadrat Medio y Point Quadrat.

3 Objetivo 3. Tecnológico

3.1 Cobertura dronQ ~ quadrats

3.1.1 Summary values

Table 3.1: Cobertura || Summary
metodo	mean	sd	se	cv	median	min	max	n
dronQ	23.55	21.01	2.14	89.23	15.74	0.96	92.56	96
quadrat	29.92	18.47	1.89	61.75	26.50	6.00	87.00	96

3.1.2 Comparación de métodos

Los datos no son normales (W = 0.89; p<0.0001); pero si se cumple la homocedasticidad (Bartlett’s K-squared = 1.56; p=0.2119). Aplicamos una comparación no paramétrica (Wilcoxon Test), y observamos que existen diferencias significativas entre los valores de cobertura estimados en los quadrats frente a los estimados por el dronQ (Tabla 3.2). La cobertura estimada por quadrat presentan valores de la mediana superiores a los estimados con dronQ (Figura 3.1).

Table 3.2: DronQ ~ Quadrat || Wilcoxon Comparison test
statistic	p.value	method	alternative
3248.5	<0.001	Wilcoxon rank sum test with continuity correction	two.sided

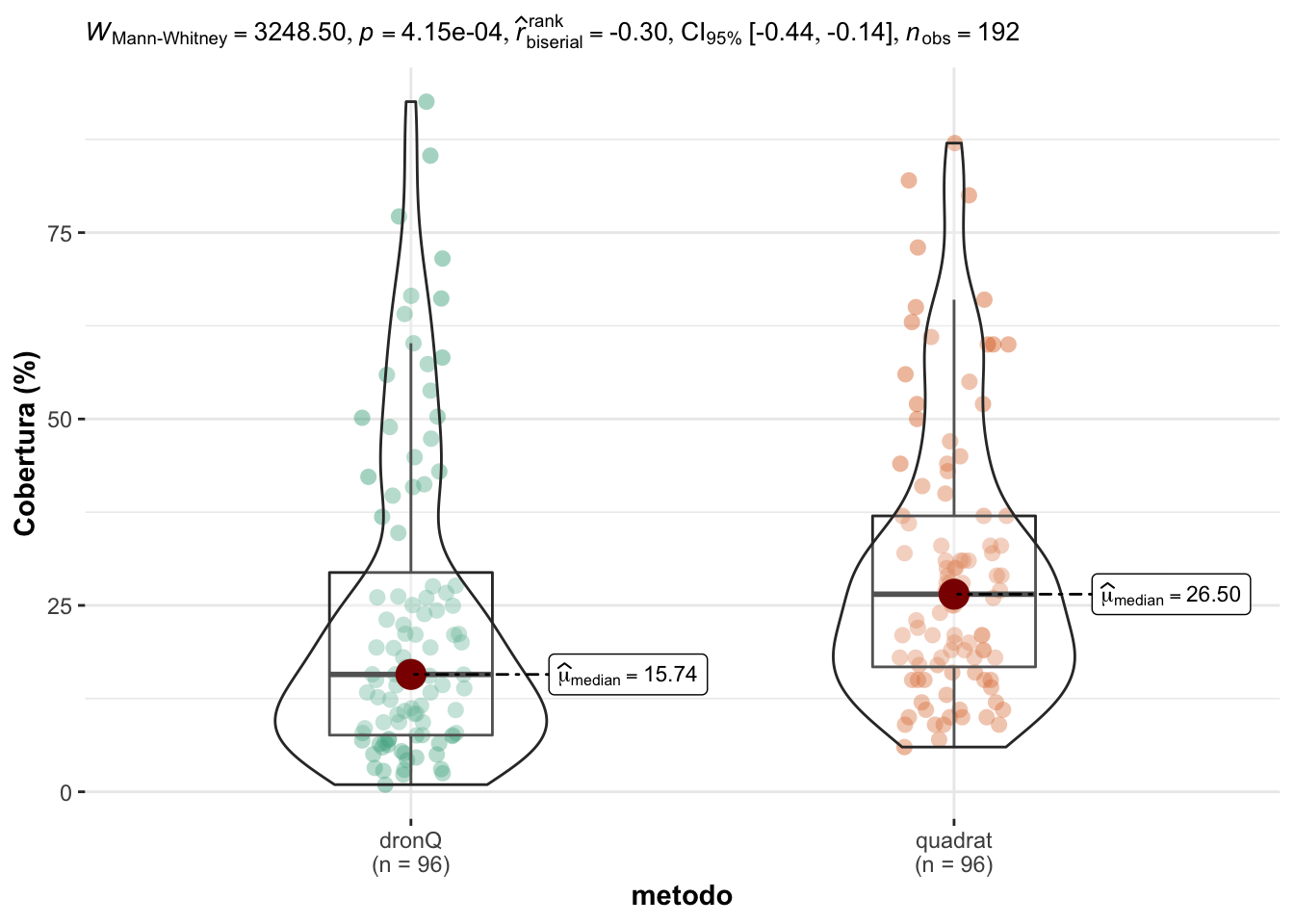
Figure 3.1: Comparación de los valores de cobertura entre DronQ y Quadrat.

3.1.3 Correlación

Observamos una alta correlación significativa entre los valores de cobertura estimados por dronQ y los estimados en campo por los quadrats (\(R^2=\) 0.82) (3.2, aunque observamos que el quadrat sobreestima los valores dados por el dronQ. Asimismo observamos un valor de RMSE de 10.86 (y un valor de RMSE normalizado de 13.41) (Tabla 3.3).

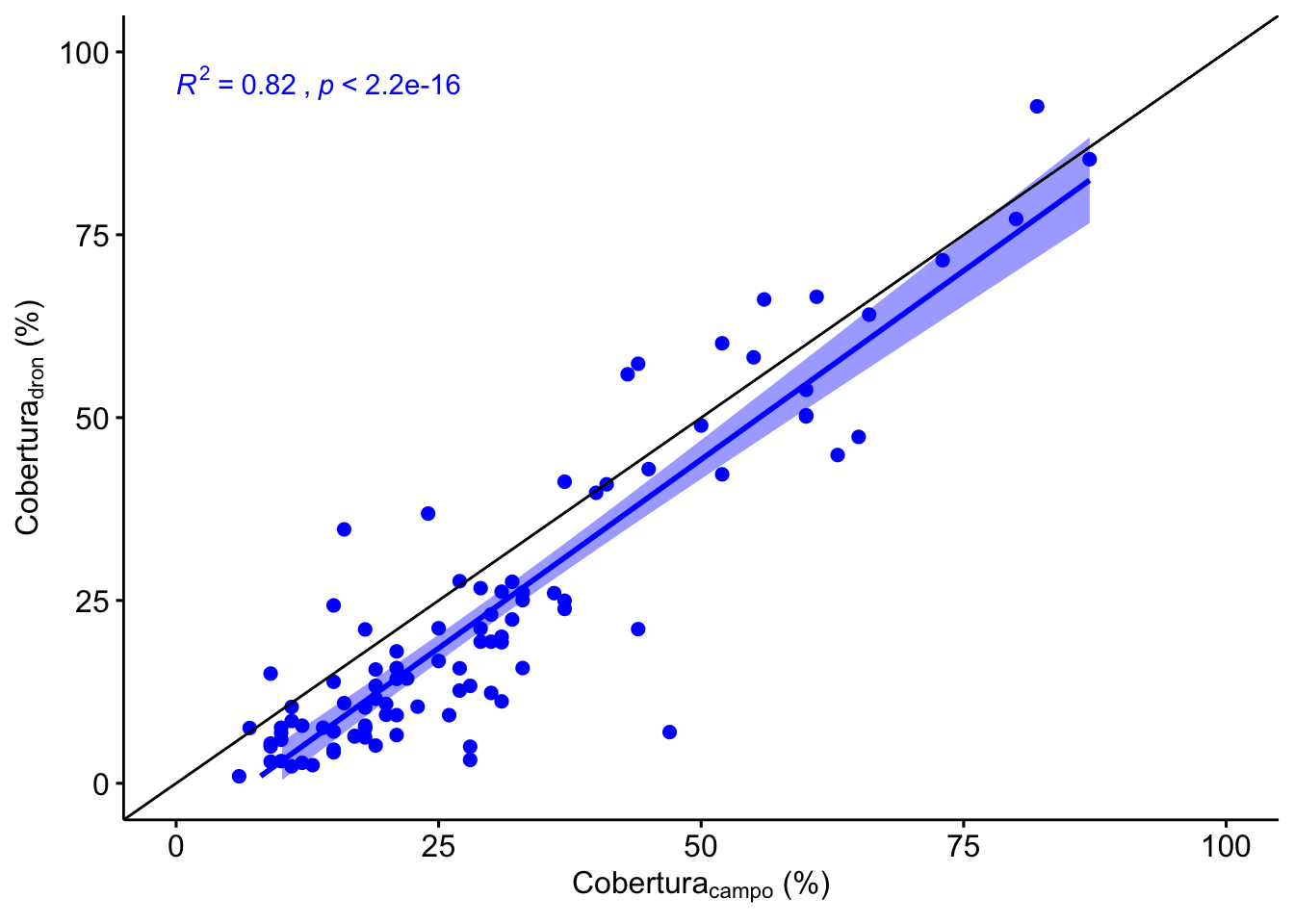
Figure 3.2: Correlación entre los valores de cobertura estimados por dronQ y Quadrat.

Table 3.3: Cobertura || RMSE
rmse	min	max	rmsen.minmax
10.86	6	87	13.41

3.1.3.1 Partición de la varianza

¿Es la relación entre dronQ-Quadrat uniforme a lo largo de todos los valores de cobertura o existen grupos dentro de esta correlación? Dicho de otro modo, ¿la correlación entre las dos variables es homogénea a lo largo de todos los valores de cobertura?. Para ello aplicamos una técnica de partición de la varianza, y hacemos árboles de clasificación.


Model formula:
dronQ ~ quadrat

Fitted party:
[1] root
|   [2] quadrat <= 37
|   |   [3] quadrat <= 23
|   |   |   [4] quadrat <= 14: 6.028 (n = 17, err = 199.7)
|   |   |   [5] quadrat > 14: 11.864 (n = 27, err = 1197.2)
|   |   [6] quadrat > 23: 20.458 (n = 29, err = 1988.0)
|   [7] quadrat > 37
|   |   [8] quadrat <= 52: 41.624 (n = 10, err = 2476.0)
|   |   [9] quadrat > 52: 63.698 (n = 13, err = 2668.2)

Number of inner nodes:    4
Number of terminal nodes: 5

$`1`
               quadrat
statistic 7.825365e+01
p.value   9.062347e-19

$`2`
               quadrat
statistic 3.184656e+01
p.value   1.668448e-08

$`3`
              quadrat
statistic 6.645925944
p.value   0.009938281

$`4`
NULL

$`5`
             quadrat
statistic 0.01297757
p.value   0.90930188

$`6`
             quadrat
statistic 3.81413871
p.value   0.05082173

$`7`
               quadrat
statistic 1.231918e+01
p.value   4.483287e-04

$`8`
NULL

$`9`
NULL

Los resultados indican Nos indica que existen al menos 5 grupos (Figura 3.3. Sin embargo, podemos estar sobreparametrizando. Para ello evaluamos si existe overfitting:

Hacer crecer un árbol sobre cierto nivel de complejidad, puede llevarnos a sobreparametrizar el modelo. ¿En que nodo cortamos el árbol?
Es preferible tener un modelo más simple que sobreparametrizar el ajuste. Para ello podemos utilizar el Complexity parameter (CP), que controla el tamaño del árbol de decisión. Si el coste de añadir otro nodo (u otra variable) a partir del nodo actual está por encima del valor del cp, entonces el árbol no continúa creciendo. Mas información aquí.

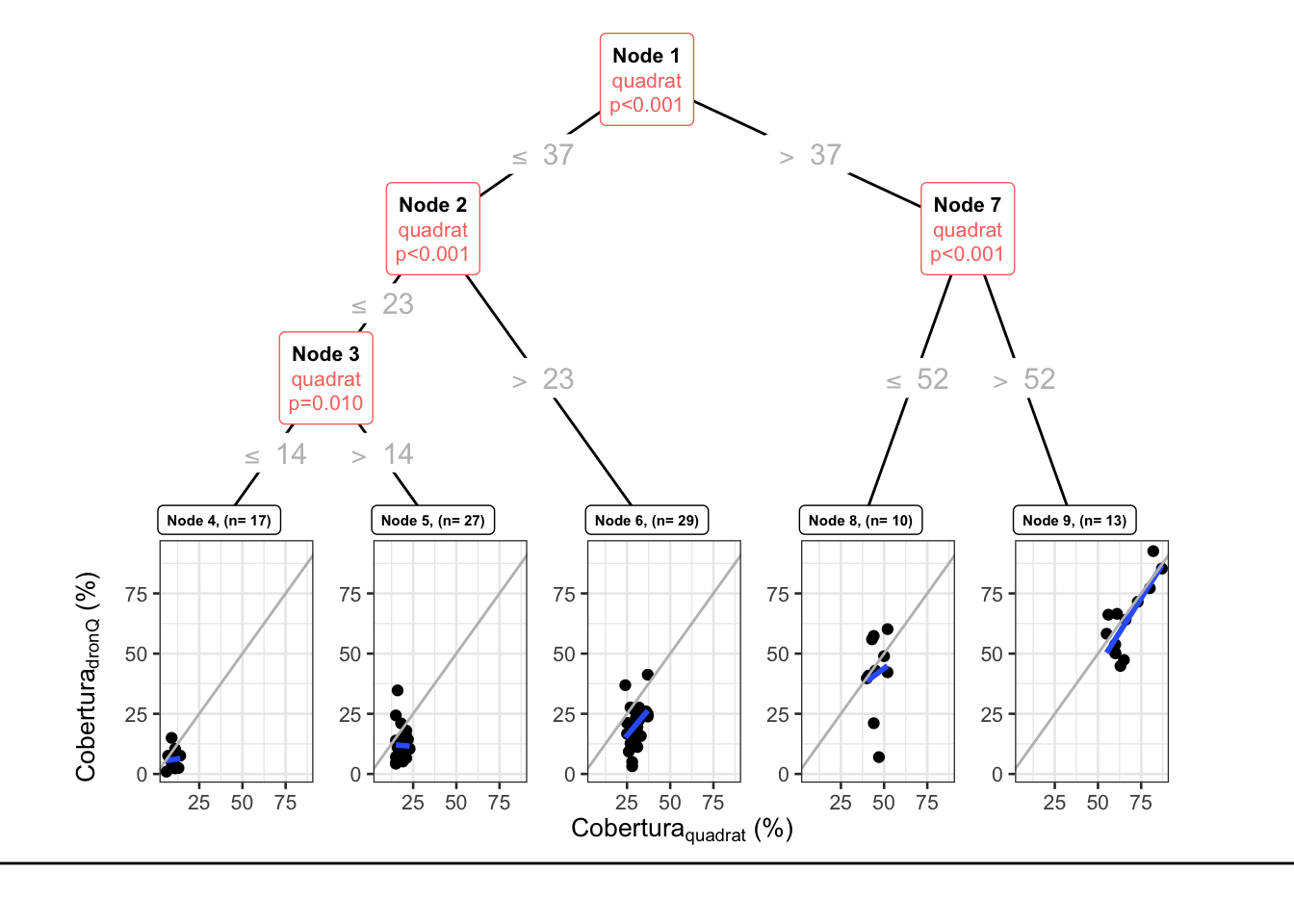
Figure 3.3: Relación entre la cobertura estimada con DronQ y con Quadrat. Partición de la varianza (modelo global)


Regression tree:
rpart(formula = dronQ ~ quadrat, data = dfcob_dronq)

Variables actually used in tree construction:
[1] quadrat

Root node error: 41934/96 = 436.82

n= 96 

        CP nsplit rel error  xerror     xstd
1 0.673397      0   1.00000 1.02574 0.179216
2 0.065679      1   0.32660 0.41939 0.092489
3 0.049060      2   0.26092 0.43811 0.088174
4 0.010000      3   0.21186 0.32548 0.065304

Table 3.4: CP Error - Modelo global Cobertura
CP	nsplit	rel error	xerror	xstd
0.6734	0	1.000	1.026	0.1792
0.0657	1	0.327	0.419	0.0925
0.0491	2	0.261	0.438	0.0882
0.0100	3	0.212	0.325	0.0653

Al explorar este modelo observamos que el error (xerror) (Tabla 3.4) no se disminuye sustancialmente a partir del 3 item (nsplit = 2) (Figura 3.4). Por tanto volvemos a modelar, usando un cp = 0.22.

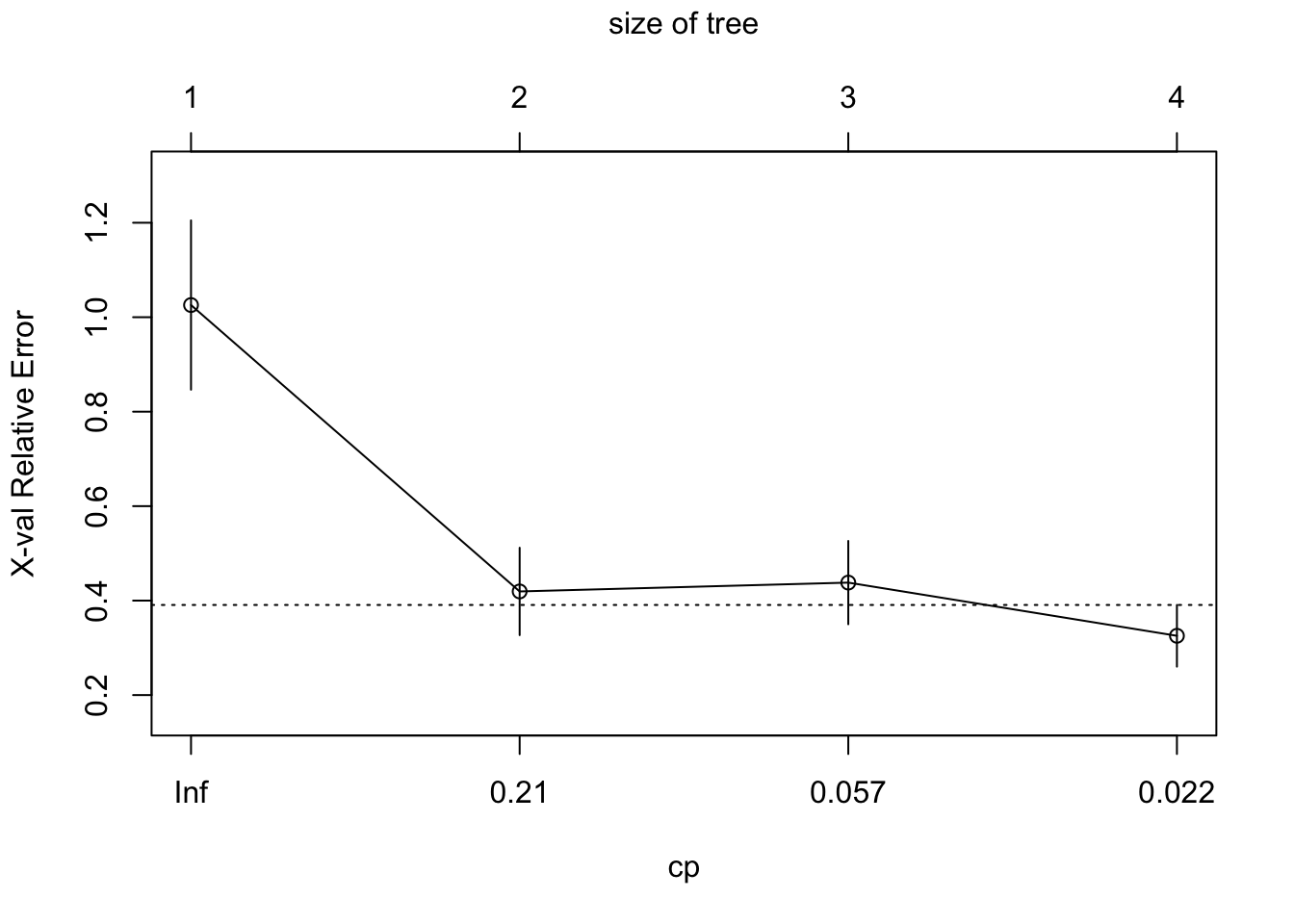
Figure 3.4: Error relativo frente a CP del modelo de partición de la varianza completo de la cobertura


Regression tree:
rpart(formula = dronQ ~ quadrat, data = dfcob_dronq, control = rpart.control(minsplit = 2, 
    cp = 0.22))

Variables actually used in tree construction:
[1] quadrat

Root node error: 41934/96 = 436.82

n= 96 

      CP nsplit rel error  xerror     xstd
1 0.6734      0    1.0000 1.02574 0.179216
2 0.2200      1    0.3266 0.41939 0.092489

Table 3.5: CP Error - Modelo global Cobertura
CP	nsplit	rel error	xerror	xstd
0.6734	0	1.000	1.026	0.1792
0.2200	1	0.327	0.419	0.0925

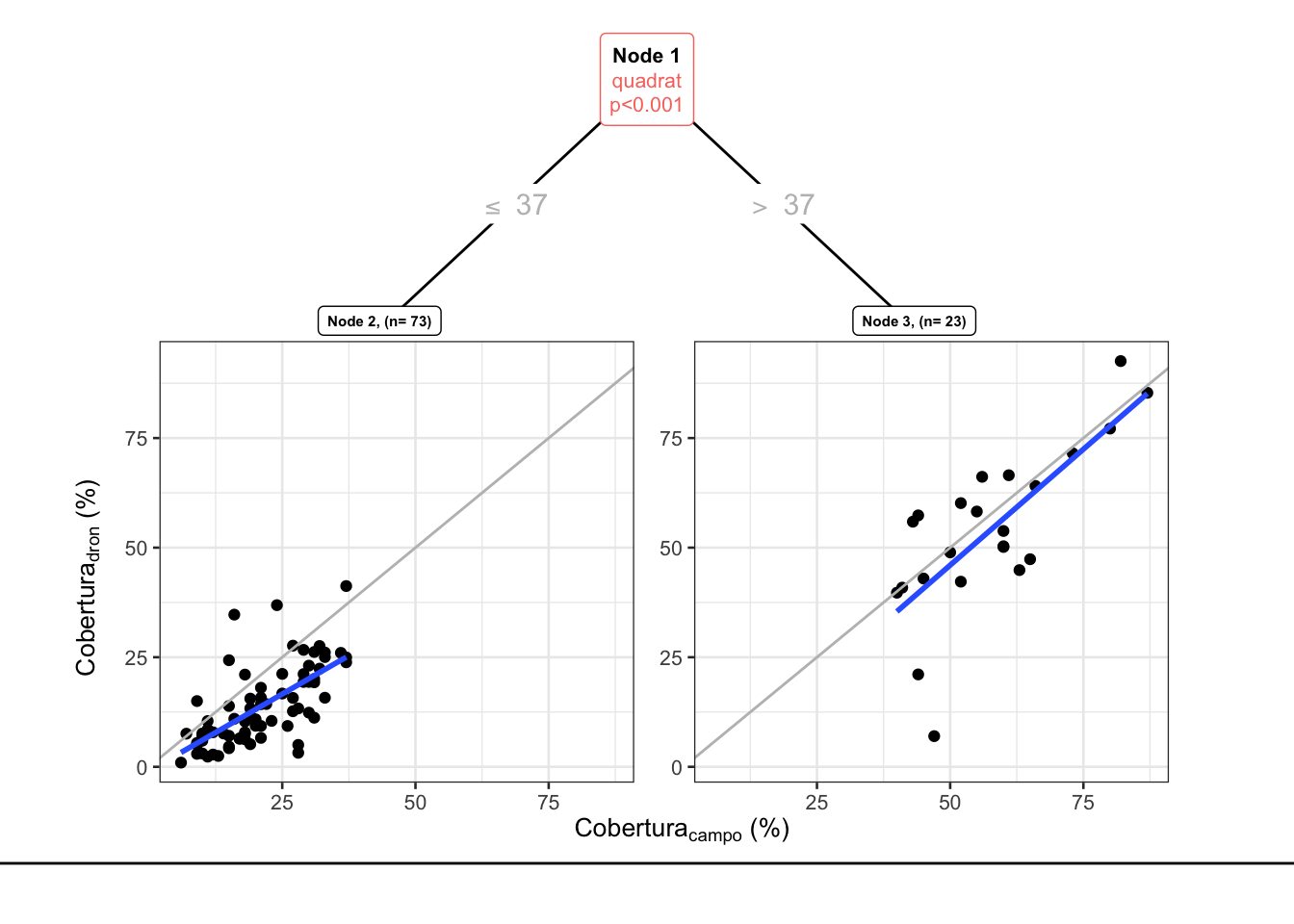
Figure 3.5: Relación entre la cobertura estimada con DronQ y con Quadrat. Partición de la varianza (modelo final)

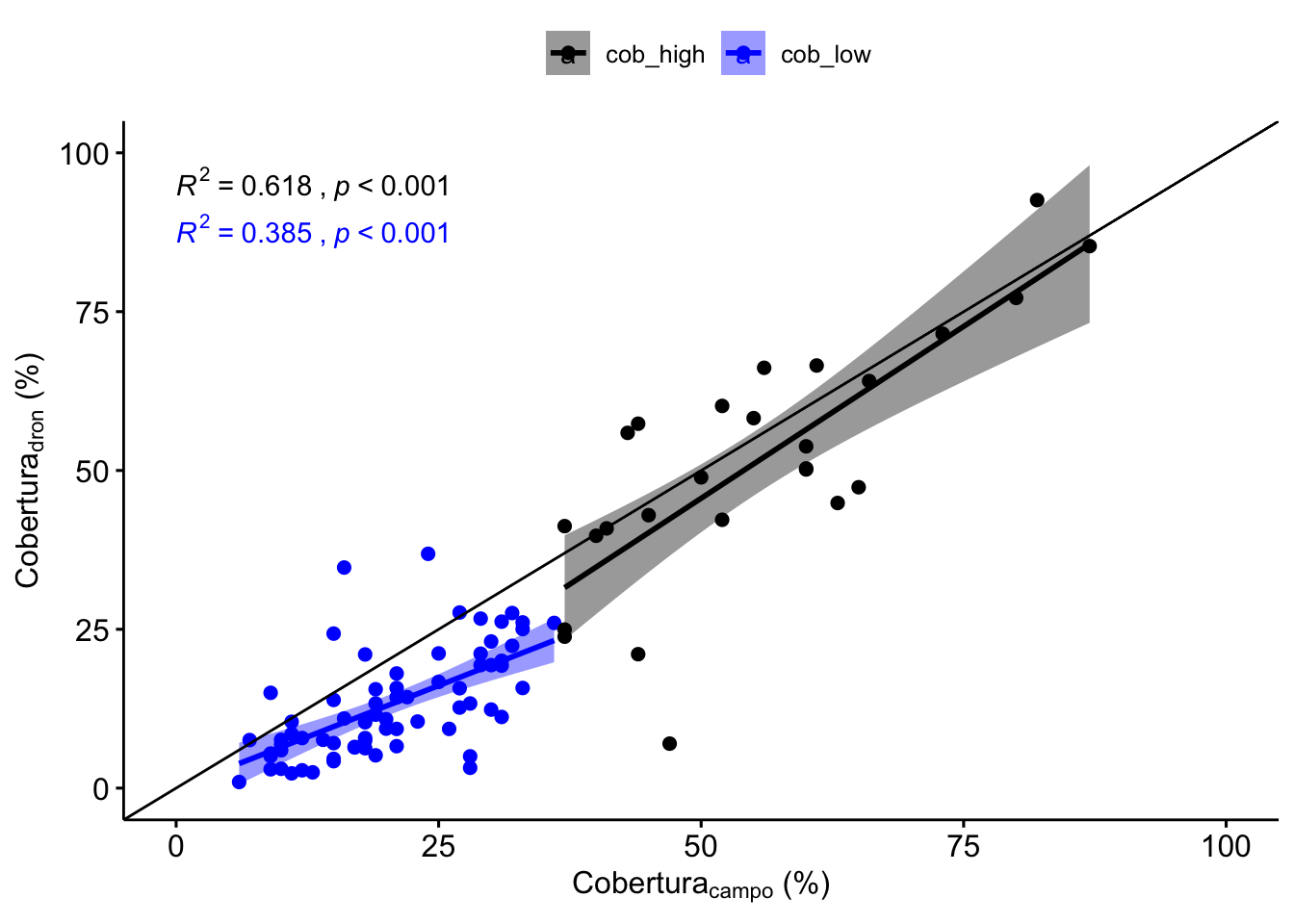
Correlación entre los valores de cobertura estimados por dronQ y Quadrat, considerando dos grupos (Coberturas inferiores (azul) y superiores (negro) a 36 % (en campo).

Figure 3.6: Correlación entre los valores de cobertura estimados por dronQ y Quadrat, considerando dos grupos (Coberturas inferiores (azul) y superiores (negro) a 36 % (en campo).

Table 3.6: Cobertura (por grupos) || RMSE
clase	rmse	min	max	rmsen.minmax
cob_high	12.58	37	87	25.16
cob_low	10.15	6	36	33.82

3.2 Cobertura dronT ~ LI y PQ

3.2.1 Summary values

Table 3.7: Cobertura dron Parcela || Summary
metodo	mean	sd	se	cv	median	min	max	n
line_intercept	27.19	6.49	1.87	23.86	29.67	11.95	34.00	12
point_quadrat	55.50	7.62	2.20	13.73	56.00	41.00	64.00	12
dronT	17.46	2.71	0.78	15.51	17.07	14.29	22.92	12

3.2.2 Comparación de métodos

ANOVA Kruskal Wallis

Table 3.8: Cobertura Parcela || Non-parametric Kruskal-Wallis ANOVA
statistic	p.value	parameter	method	mi_variable
27.90057	9e-07	2	Kruskal-Wallis rank sum test	cobertura

Posteriormente, evaluamos si existen diferencias entre cada uno de los métodos (post hoc) y observamos que existen diferencias significativas entre el point quadrat y los otros métodos (line intercept y dron Parcela) (Tabla 3.9, Figura 3.7). Asimismo, no observamos diferencias entre la cobertura estimada según el line intercept y el dron Parcela.

Table 3.9: Cobertura Parcela || Non-parametric Kruskal-Wallis ANOVA - Post-hoc Dunn’s-test with Bonferroni adjustment
H0	statistic	p.value
line_intercept = point_quadrat	3.12	0.005
line_intercept = dronT	2.13	0.099
point_quadrat = dronT	5.25	<0.001

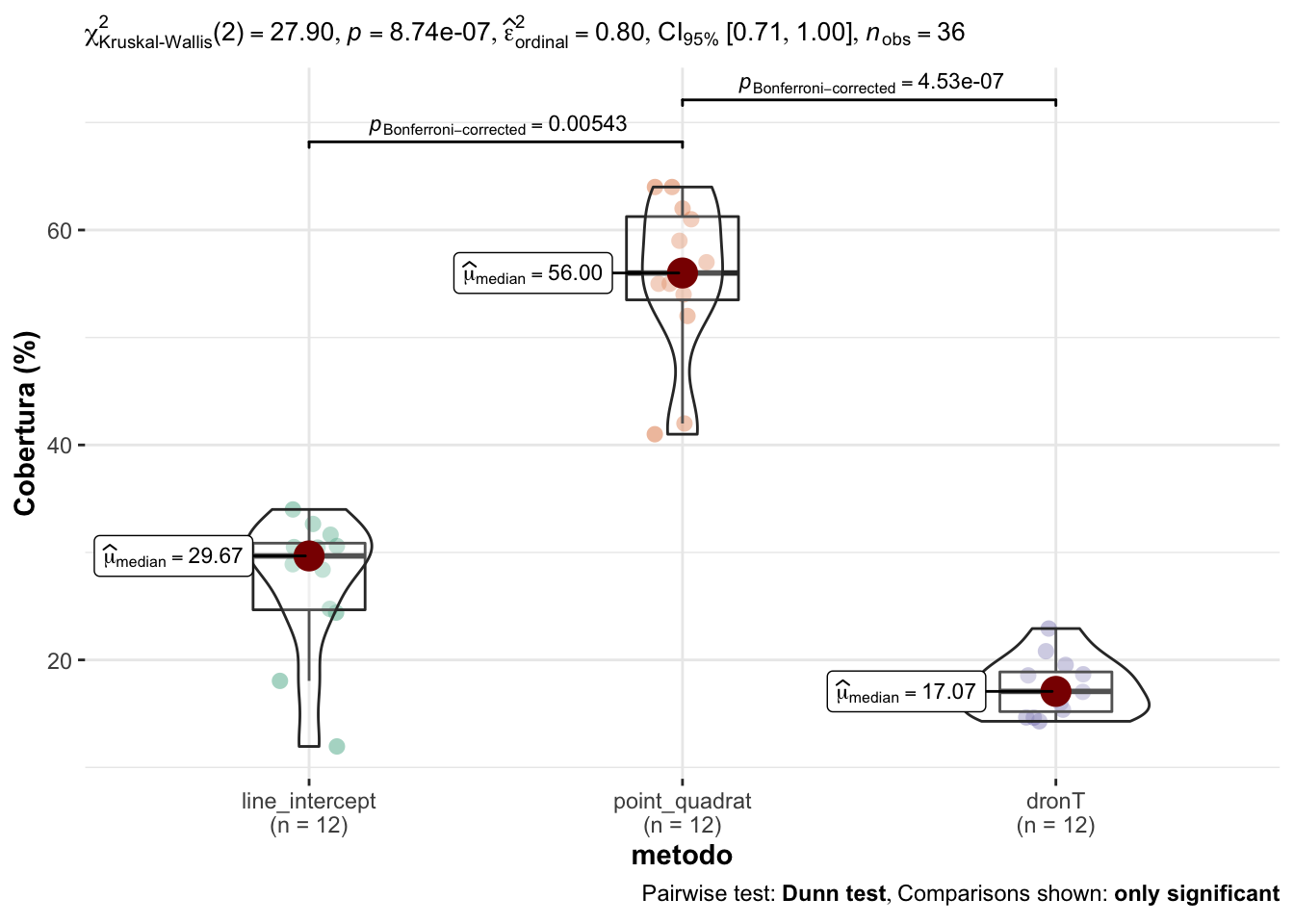
Figure 3.7: Comparación de los valores de cobertura entre los diferentes métodos de campo.

3.2.3 Correlación

Tanto line intercept como point quadrat subestiman los valores de cobertura dados por el dron en la parcela de 500 m^2 (Figura 3.8). Independientemente no presentan buenas correlaciones con el valor de cobertura estimado por el dron para toda la parcela.

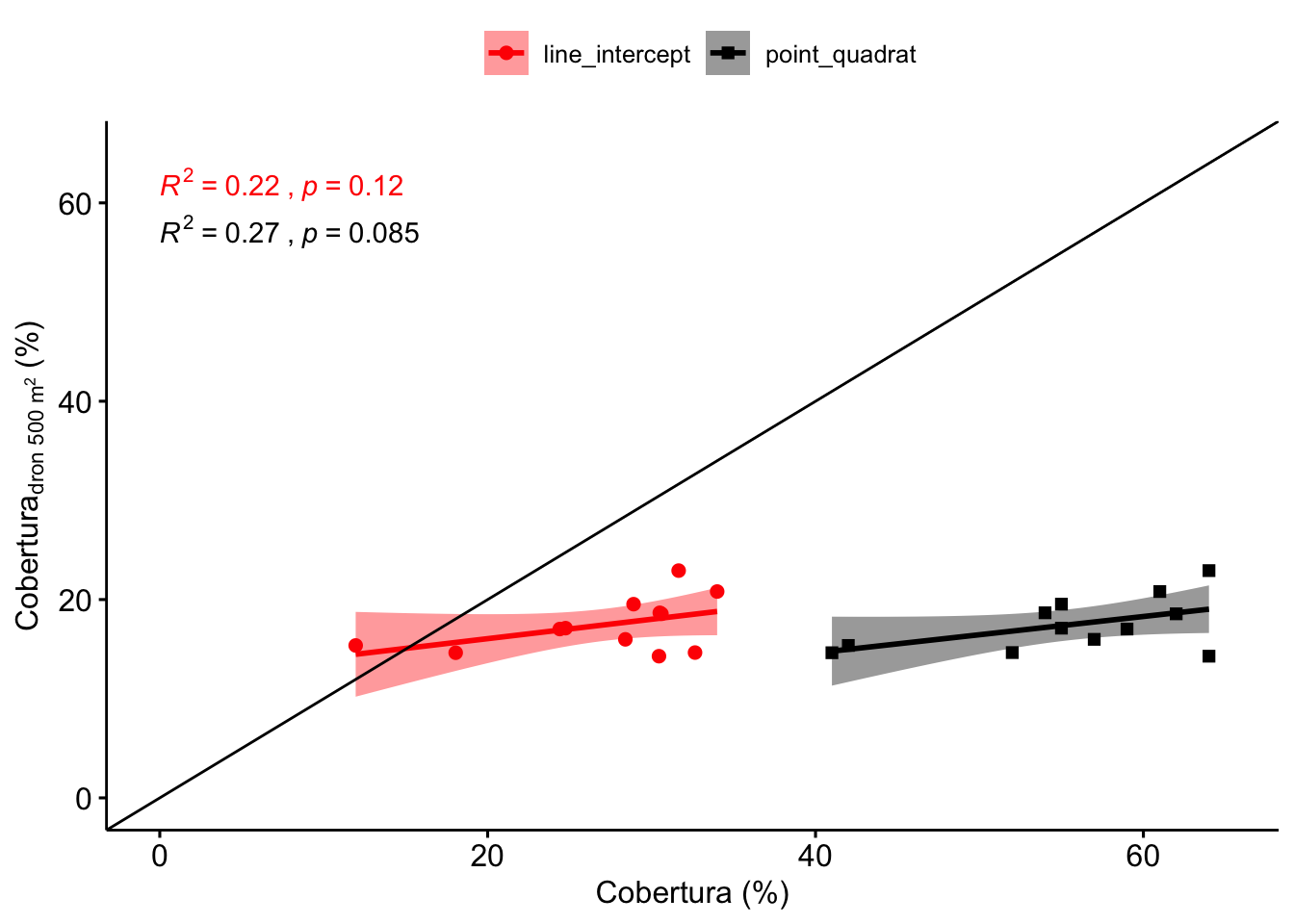
Figure 3.8: Correlación entre los valores de cobertura estimados por dronParcela con respecto a Line Intercept y Point Quadrat.

3.3 Fitovolumen dronQ ~ quadrats

3.3.1 Summary values

Table 3.10: Fitovolumen || Summary
metodo	mean	sd	se	cv	median	min	max	n
dronQ	421.70	678.47	69.25	160.89	125.9	1.75	4077.36	96
quadrat	778.57	1108.78	113.16	142.41	323.4	28.05	5690.30	96

3.3.2 Comparación de métodos

Los datos no son normales (W = 0.63; p<0.0001) ni homocedasticos (Bartlett’s K-squared = 21.94; p<0.0001). Aplicamos una comparación no paramétrica (Wilcoxon Test), y observamos que existen diferencias significativas entre los valores de fitovolumen estimados en los quadrats frente a los estimados por el dronQ (Tabla 3.11). La cobertura estimada por quadrat presentan valores de la mediana superiores a los estimados con dronQ (Figura 3.9).

Table 3.11: Fitovolumen DronQ ~ Quadrat || Wilcoxon Comparison test
statistic	p.value	method	alternative
2965	<0.001	Wilcoxon rank sum test with continuity correction	two.sided

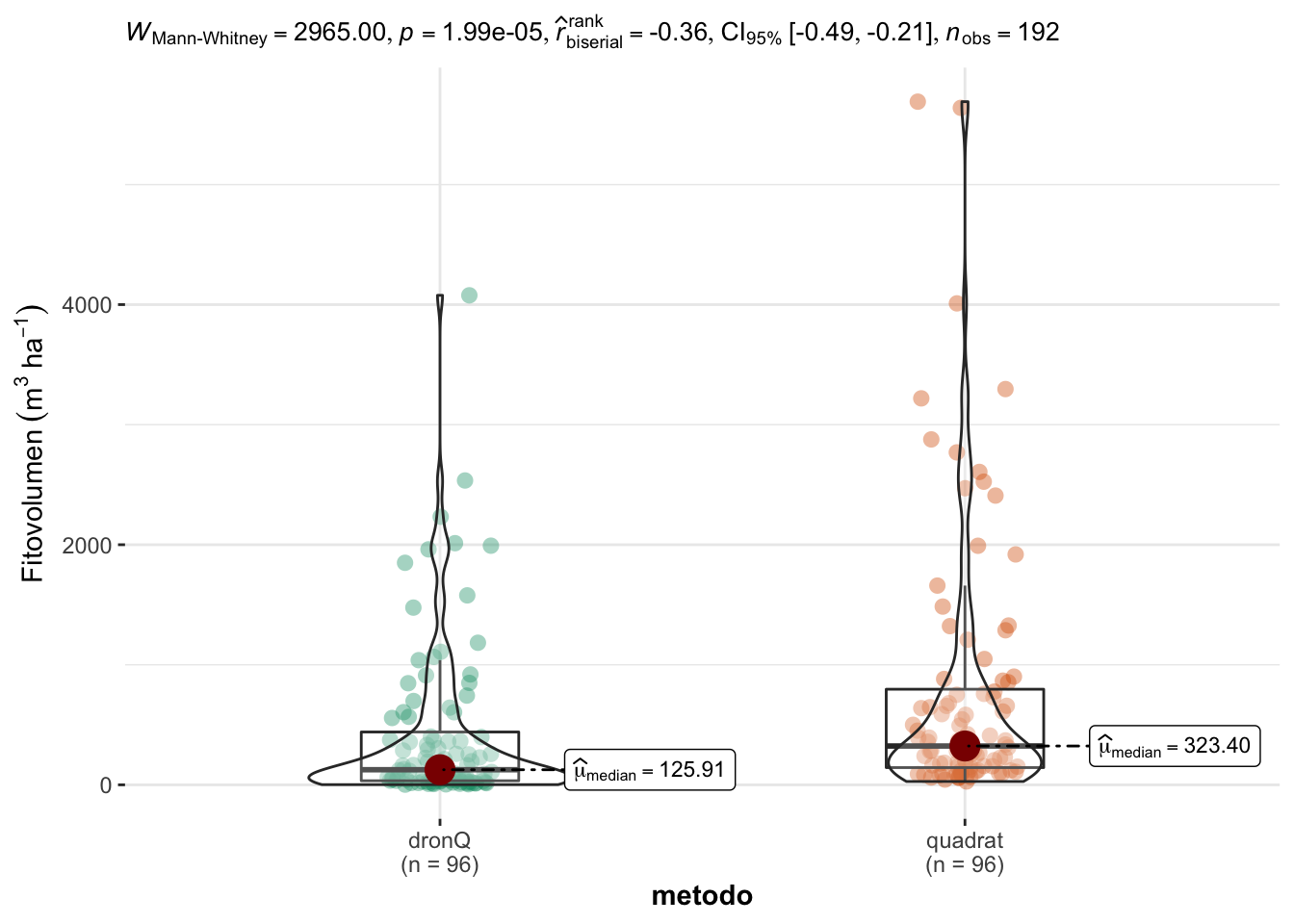
Figure 3.9: Comparación de los valores de fitovolumen entre DronQ y Quadrat.

3.3.3 Correlación

Observamos una alta correlación significativa entre los valores de fitovolumen estimados por dronQ y los estimados en campo por los quadrats (\(R^2=\) 0.9) (3.10, aunque observamos que el quadrat sobreestima los valores dados por el dronQ. Los valores de RMSE son de 619.49 (y un valor de RMSE normalizado de 10.94) (Tabla 3.12).

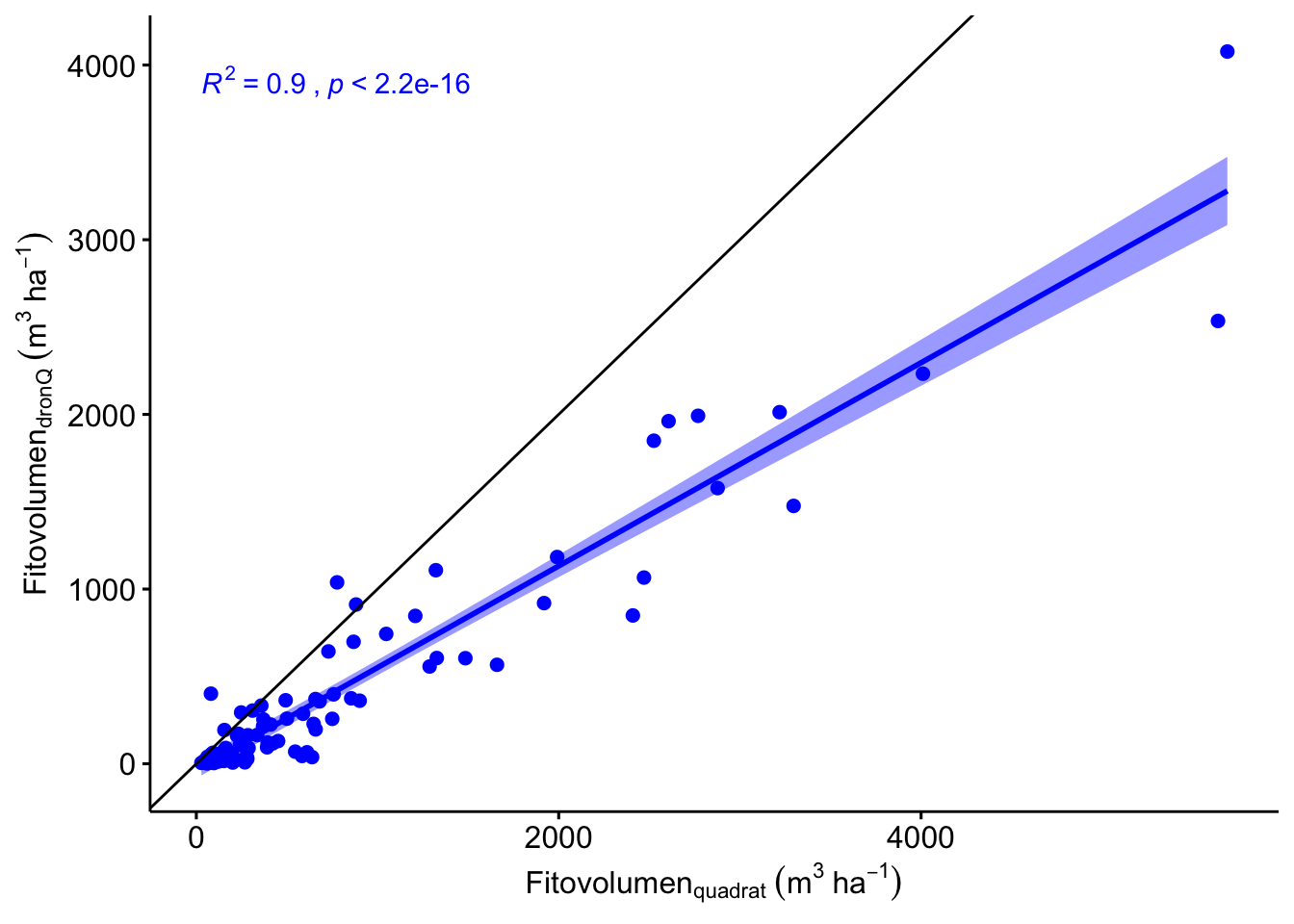
Figure 3.10: Correlación entre los valores de fitovolumen estimados por dronQ y Quadrat.

Table 3.12: Fitovolumen || RMSE
rmse	min	max	rmsen.minmax
619.49	28	5690	10.94

3.3.3.1 Partición de la varianza


Model formula:
dronQ ~ quadrat

Fitted party:
[1] root
|   [2] quadrat <= 2470.6
|   |   [3] quadrat <= 680.3
|   |   |   [4] quadrat <= 288.3: 59.556 (n = 47, err = 276365.7)
|   |   |   [5] quadrat > 288.3: 201.746 (n = 21, err = 240180.9)
|   |   [6] quadrat > 680.3: 722.725 (n = 19, err = 1345456.4)
|   [7] quadrat > 2470.6: 2190.586 (n = 9, err = 4805690.0)

Number of inner nodes:    3
Number of terminal nodes: 4

$`1`
               quadrat
statistic 8.589206e+01
p.value   1.900300e-20

$`2`
               quadrat
statistic 6.339813e+01
p.value   1.688783e-15

$`3`
               quadrat
statistic 2.170388e+01
p.value   3.181471e-06

$`4`
             quadrat
statistic 3.03838023
p.value   0.08131702

$`5`
              quadrat
statistic 0.006282002
p.value   0.936826555

$`6`
NULL

$`7`
NULL

Los resultados indican Nos indica que existen al menos 4 grupos (Figura 3.11. Sin embargo, podemos estar sobreparametrizando. Para ello evaluamos si existe overfitting:

Hacer crecer un árbol sobre cierto nivel de complejidad, puede llevarnos a sobreparametrizar el modelo. ¿En que nodo cortamos el árbol?
Es preferible tener un modelo más simple que sobreparametrizar el ajuste. Para ello podemos utilizar el Complexity parameter (CP), que controla el tamaño del árbol de decisión. Si el coste de añadir otro nodo (u otra variable) a partir del nodo actual está por encima del valor del cp, entonces el árbol no continúa creciendo. Mas información aquí.

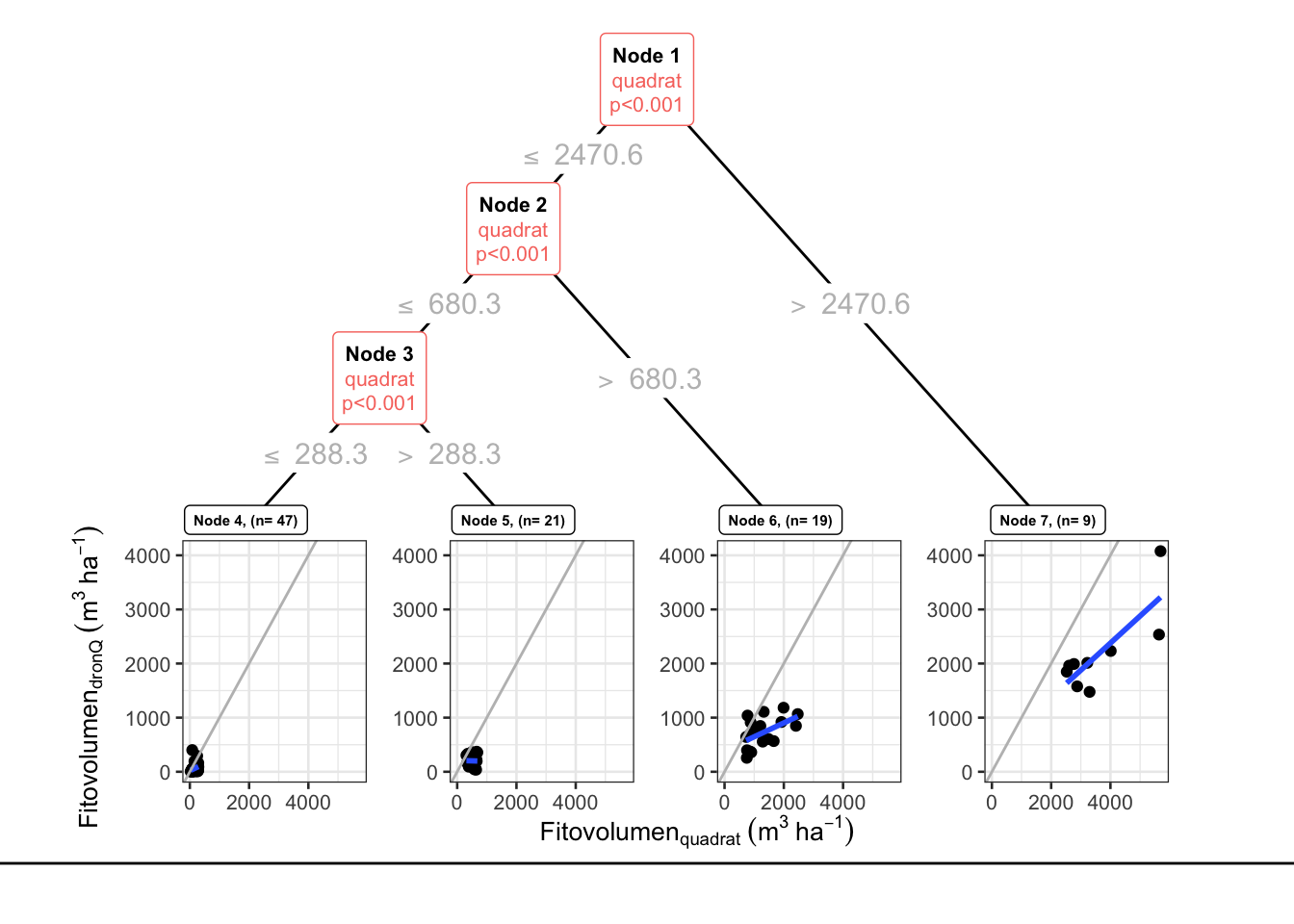
Figure 3.11: Relación entre el fitovolumen estimado con DronQ y con Quadrat. Partición de la varianza (modelo global)


Regression tree:
rpart(formula = dronQ ~ quadrat, data = dffit_dronq)

Variables actually used in tree construction:
[1] quadrat

Root node error: 43729935/96 = 455520

n= 96 

       CP nsplit rel error  xerror    xstd
1 0.71059      0   1.00000 1.01996 0.34309
2 0.13023      1   0.28941 0.42441 0.14781
3 0.01000      2   0.15919 0.30462 0.13893

Table 3.13: CP Error - Modelo global Fitvolumen
CP	nsplit	rel error	xerror	xstd
0.7106	0	1.000	1.020	0.3431
0.1302	1	0.289	0.424	0.1478
0.0100	2	0.159	0.305	0.1389

Al explorar este modelo observamos que el error (xerror) (Tabla 3.13) no se disminuye sustancialmente a partir del 2 item (nsplit = 1) (Figura 3.12). Por tanto volvemos a modelar, usando un cp = 0.3.

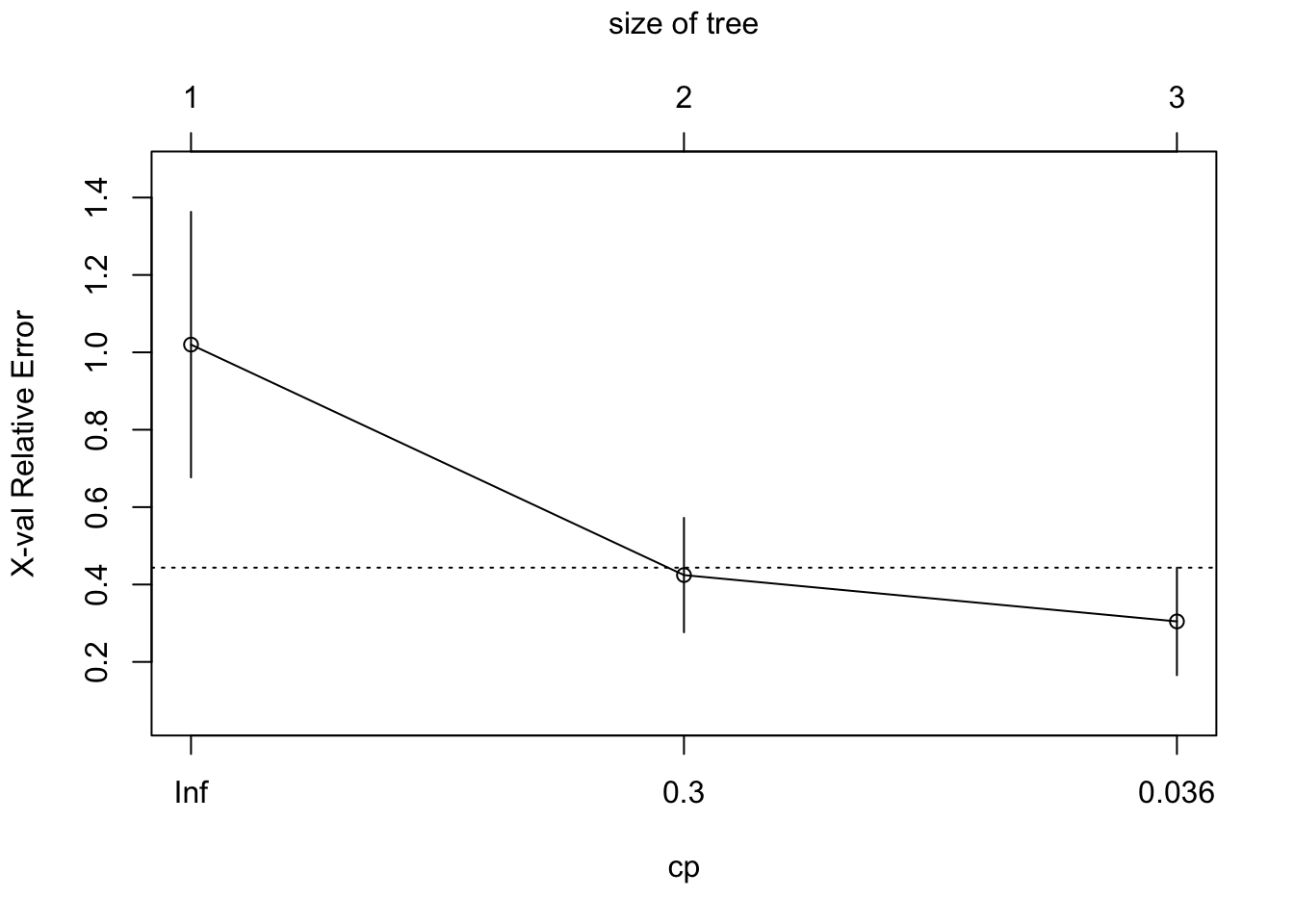
Figure 3.12: Error relativo frente a CP del modelo de partición de la varianza completo del fitovolumen


Regression tree:
rpart(formula = dronQ ~ quadrat, data = dffit_dronq, control = rpart.control(minsplit = 2, 
    cp = 0.3))

Variables actually used in tree construction:
[1] quadrat

Root node error: 43729935/96 = 455520

n= 96 

       CP nsplit rel error  xerror    xstd
1 0.71059      0   1.00000 1.01996 0.34309
2 0.30000      1   0.28941 0.42441 0.14781

Table 3.14: CP Error - Modelo global Fitovolumen
CP	nsplit	rel error	xerror	xstd
0.7106	0	1.000	1.020	0.3431
0.3000	1	0.289	0.424	0.1478

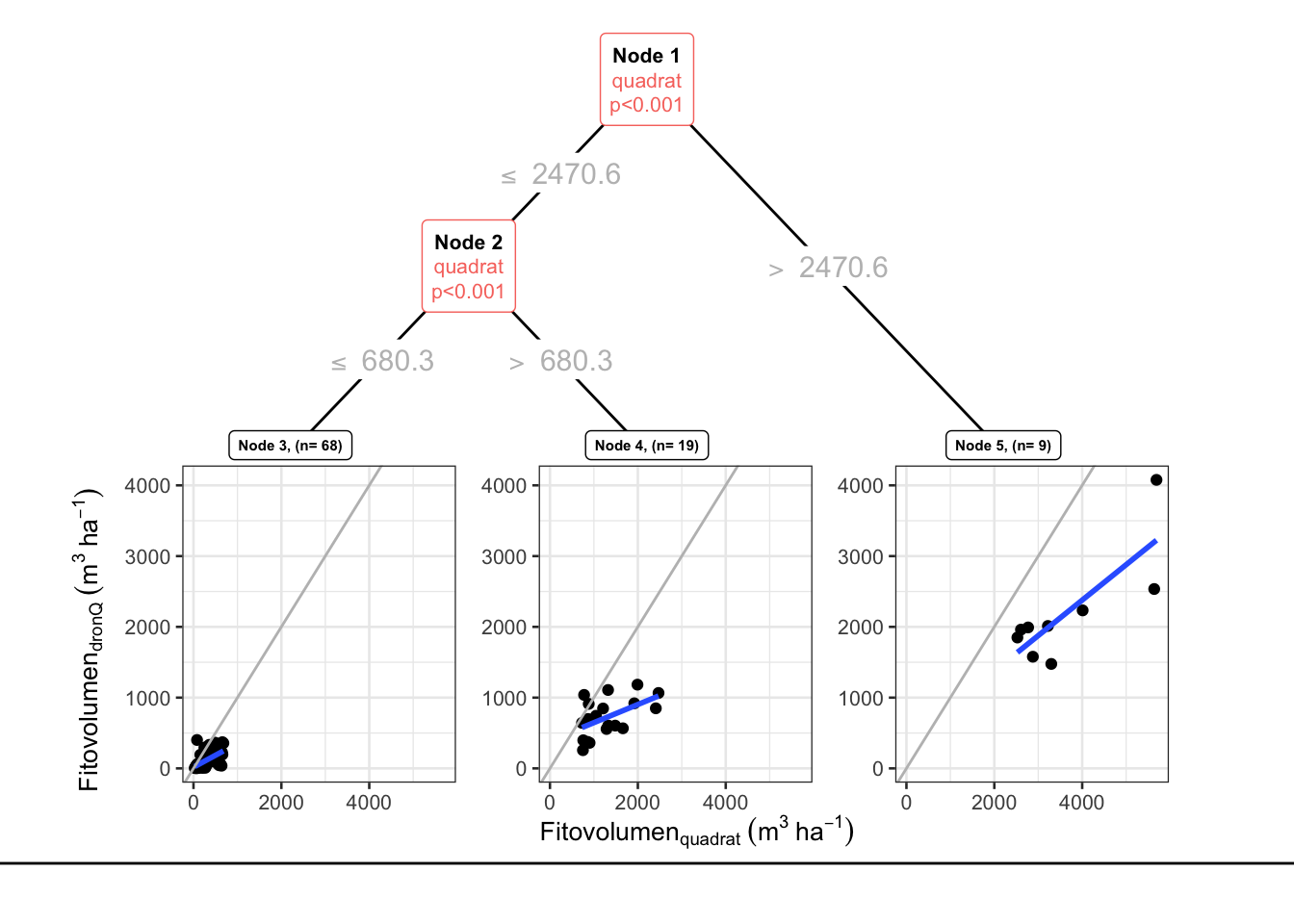
Figure 3.13: Relación entre el fitovolumen estimado con DronQ y con Quadrat. Partición de la varianza (modelo final)

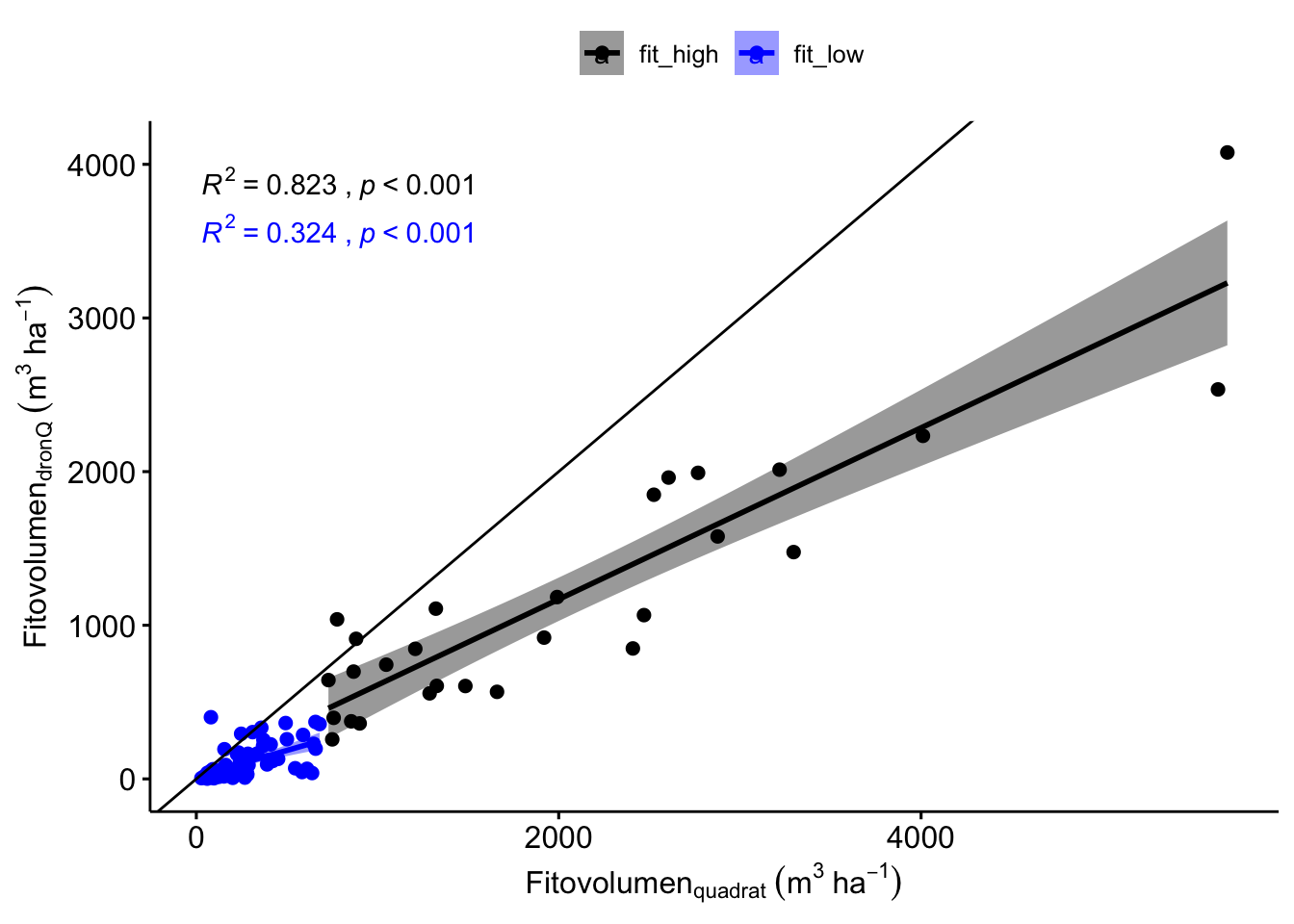
Correlación entre los valores de fitovolumen estimados por dronQ y Quadrat, considerando dos grupos (Fitovolumen inferiores (azul) y superiores (negro) a 681 % (en campo).

Figure 3.14: Correlación entre los valores de fitovolumen estimados por dronQ y Quadrat, considerando dos grupos (Fitovolumen inferiores (azul) y superiores (negro) a 681 % (en campo).

Table 3.15: Fitovolumen (por grupos) || RMSE
clase	rmse	min	max	rmsen.minmax
fit_high	1096.73	729	5690	22.11
fit_low	215.68	28	680	33.07

3.4 Fitovolumen dronT ~ LI

3.4.1 Summary values

Table 3.16: Fitovolumen dron Parcela || Summary
metodo	mean	sd	se	cv	median	min	max	n
dronT	450.63	141.74	40.92	31.45	408.39	286.29	681.28	12
line_intercept	531.04	274.90	79.36	51.77	543.13	84.27	1016.86	12

3.4.2 Comparación de métodos

Los datos son normales (W = 0.97; p=0.7087); pero no se cumple la homocedasticidad (Bartlett’s K-squared = 4.31; p=0.0378). Aplicamos una comparación no paramétrica (Wilcoxon Test), y observamos que no existen diferencias significativas entre los valores de fitovolumen estimados en el line intercept frente a los estimados por el dronT (parcela) (Tabla 3.17; Figura 3.15).

Table 3.17: Fitovolumen DronT ~ Line Intercept || Wilcoxon Comparison test
statistic	p.value	method	alternative
59	0.478	Wilcoxon rank sum exact test	two.sided

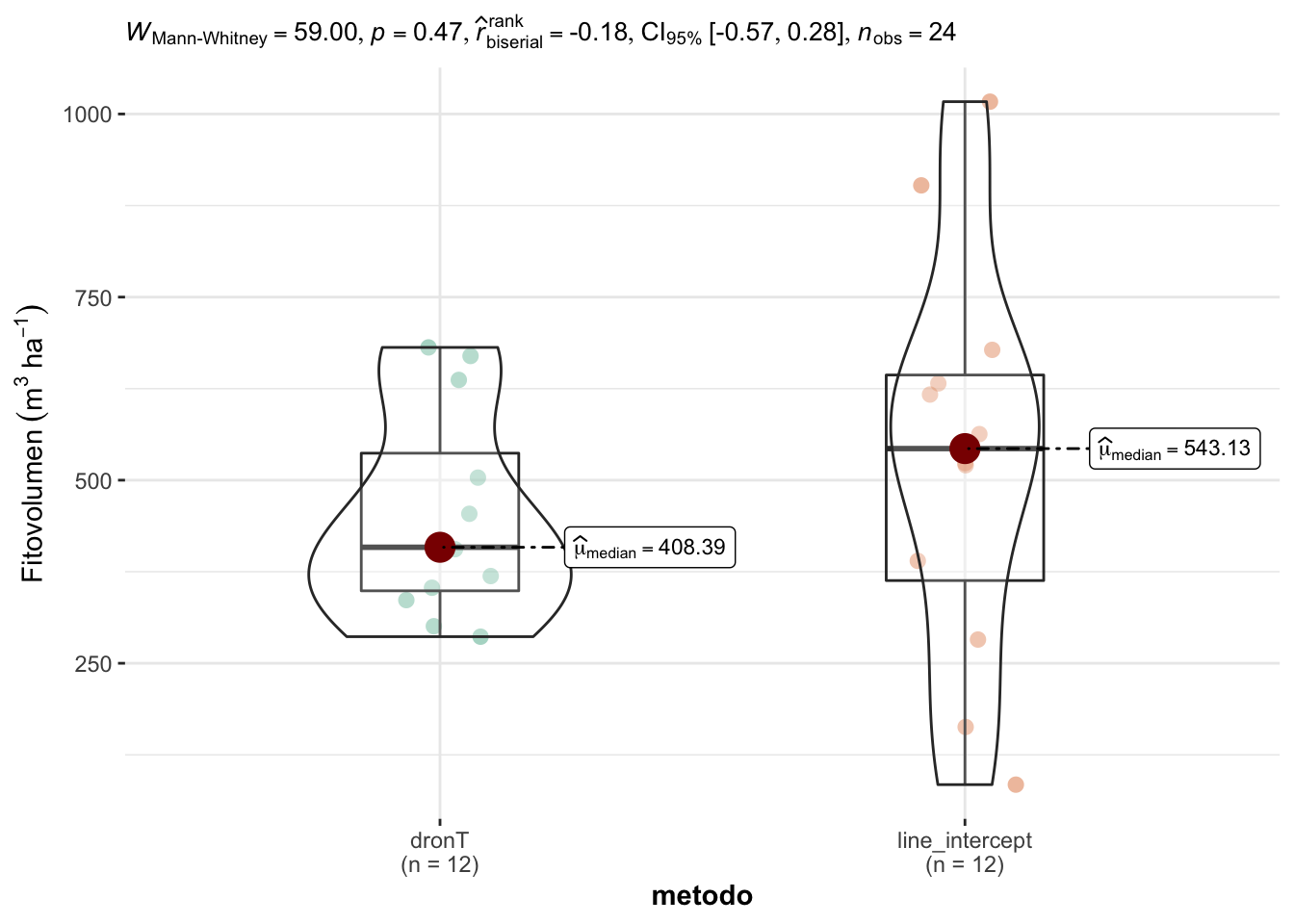
Figure 3.15: Comparación de los valores de fitovolumen entre Dron Parcela y Line Intercept.

3.4.3 Correlación

No existe una buena correlación entre los valores de fitovolumen ofrecidos por line intercept y los datos por el dron en la parcela de 500 m^2 (Figura 3.16).

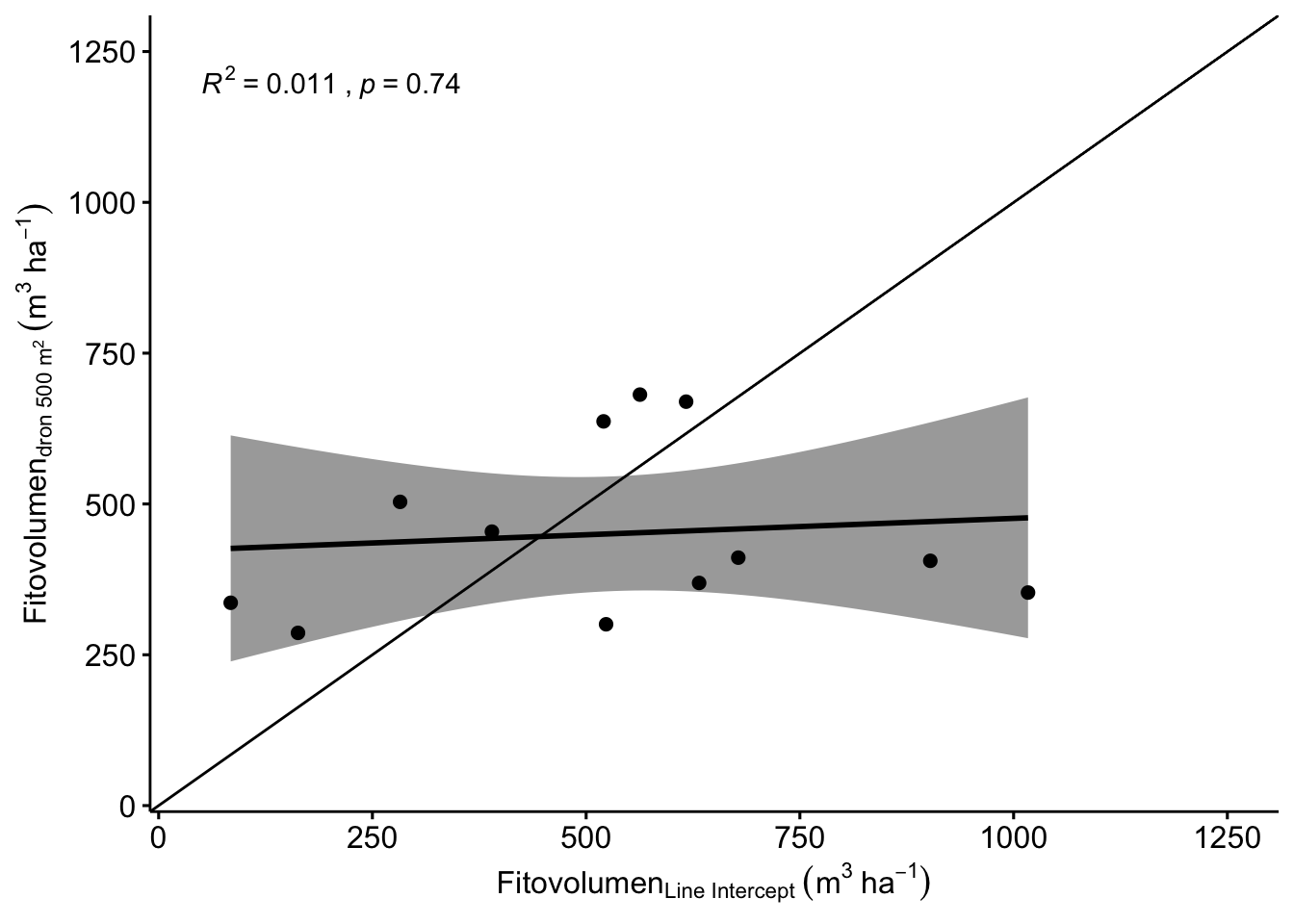
Figure 3.16: Correlación entre los valores de fitovolumen estimados por dronParcela con respecto a Line Intercept

R version 4.0.2 (2020-06-22)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS Catalina 10.15.3

Matrix products: default
BLAS:   /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRblas.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRlapack.dylib

locale:
[1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8

attached base packages:
[1] stats4    grid      stats     graphics  grDevices utils     datasets 
[8] methods   base     

other attached packages:
 [1] multcompView_0.1-8        ggparty_1.0.0            
 [3] partykit_1.2-15           libcoin_1.0-7            
 [5] party_1.3-9               strucchange_1.5-2        
 [7] sandwich_3.0-0            zoo_1.8-8                
 [9] modeltools_0.2-23         mvtnorm_1.1-1            
[11] rpart_4.1-15              statsExpressions_1.3.1   
[13] ggsignif_0.6.3            pairwiseComparisons_3.1.3
[15] ggtext_0.1.1              PMCMRplus_1.9.3          
[17] PMCMR_4.3                 statmod_1.4.36           
[19] tweedie_2.3.3             report_0.5.1             
[21] kableExtra_1.3.1          cvequality_0.2.0         
[23] performance_0.8.0         ggdist_3.0.1             
[25] Metrics_0.1.4             ggstatsplot_0.9.1        
[27] colorspace_2.0-2          ggpubr_0.4.0             
[29] ggforce_0.3.2             ggdark_0.2.1             
[31] janitor_2.1.0             here_1.0.1               
[33] forcats_0.5.1             stringr_1.4.0            
[35] dplyr_1.0.6               purrr_0.3.4              
[37] readr_1.4.0               tidyr_1.1.3              
[39] tibble_3.1.2              ggplot2_3.3.5            
[41] tidyverse_1.3.1           workflowr_1.7.0          

loaded via a namespace (and not attached):
  [1] utf8_1.1.4             tidyselect_1.1.1       gmp_0.6-2             
  [4] munsell_0.5.0          effectsize_0.6.0.1     codetools_0.2-18      
  [7] withr_2.4.1            highr_0.8              knitr_1.31            
 [10] rstudioapi_0.13        ipmisc_5.0.2           labeling_0.4.2        
 [13] emmeans_1.5.4          git2r_0.28.0           polyclip_1.10-0       
 [16] farver_2.1.0           datawizard_0.4.0       rprojroot_2.0.2       
 [19] coda_0.19-4            vctrs_0.3.8            generics_0.1.0        
 [22] TH.data_1.0-10         xfun_0.23              BWStest_0.2.2         
 [25] R6_2.5.1               BayesFactor_0.9.12-4.3 cachem_1.0.4          
 [28] reshape_0.8.8          assertthat_0.2.1       promises_1.2.0.1      
 [31] scales_1.1.1.9000      multcomp_1.4-16        gtable_0.3.0          
 [34] processx_3.5.1         rlang_0.4.12           MatrixModels_0.4-1    
 [37] zeallot_0.1.0          splines_4.0.2          rstatix_0.6.0         
 [40] prismatic_1.0.0        checkmate_2.0.0        broom_0.7.9           
 [43] yaml_2.2.1             abind_1.4-5            modelr_0.1.8          
 [46] backports_1.2.1        httpuv_1.5.5           gridtext_0.1.4        
 [49] inum_1.0-3             tools_4.0.2            bookdown_0.21.6       
 [52] ellipsis_0.3.2         jquerylib_0.1.3        WRS2_1.1-3            
 [55] Rcpp_1.0.7             plyr_1.8.6             ps_1.5.0              
 [58] pbapply_1.4-3          correlation_0.8.0      ggrepel_0.9.1         
 [61] haven_2.3.1            fs_1.5.0               magrittr_2.0.1        
 [64] data.table_1.14.0      openxlsx_4.2.3         reprex_2.0.0          
 [67] whisker_0.4            matrixStats_0.58.0     hms_1.0.0             
 [70] patchwork_1.1.1        evaluate_0.14          xtable_1.8-4          
 [73] rio_0.5.16             readxl_1.3.1           rstantools_2.1.1      
 [76] compiler_4.0.2         crayon_1.4.1           htmltools_0.5.2       
 [79] mgcv_1.8-33            mc2d_0.1-18            later_1.1.0.1         
 [82] Formula_1.2-4          lubridate_1.7.10       DBI_1.1.1             
 [85] SuppDists_1.1-9.5      kSamples_1.2-9         tweenr_1.0.1          
 [88] dbplyr_2.1.1           MASS_7.3-53            boot_1.3-26           
 [91] Matrix_1.3-2           car_3.0-10             cli_2.5.0             
 [94] parallel_4.0.2         insight_0.17.0         pkgconfig_2.0.3       
 [97] getPass_0.2-2          coin_1.4-0             foreign_0.8-81        
[100] xml2_1.3.2             paletteer_1.3.0        bslib_0.2.4           
[103] webshot_0.5.2          estimability_1.3       rvest_1.0.0           
[106] snakecase_0.11.0       distributional_0.3.0   callr_3.7.0           
[109] digest_0.6.27          parameters_0.17.0      rmarkdown_2.8         
[112] cellranger_1.1.0       curl_4.3               gtools_3.8.2          
[115] nlme_3.1-152           lifecycle_1.0.1        jsonlite_1.7.2        
[118] carData_3.0-4          viridisLite_0.4.0      fansi_0.4.2           
[121] pillar_1.6.1           lattice_0.20-41        fastmap_1.1.0         
[124] httr_1.4.2             survival_3.2-7         glue_1.4.2            
[127] bayestestR_0.11.5      zip_2.1.1              stringi_1.7.4         
[130] sass_0.3.1             rematch2_2.1.2         memoise_2.0.0         
[133] Rmpfr_0.8-2

Compara métodos de campo y dron (paper SUDOE)

ajpelu

2022-04-18